题目内容
已知梯形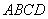 中,
中, ∥
∥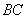 ,
,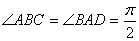 ,
,
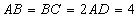 ,
,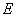 、
、 分别是
分别是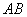 、
、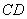 上的点,
上的点,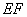 ∥
∥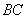 ,
, .
.
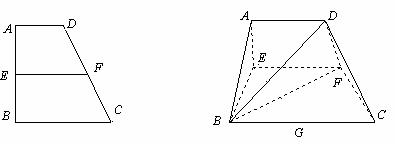
沿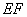 将梯形
将梯形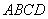 翻折,使平面
翻折,使平面 ⊥平面
⊥平面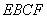 (如图).
(如图). 是
是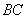 的
的
中点,以 、
、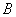 、
、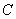 、
、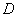 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为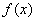 .
.
(1)当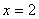 时,求证:
时,求证: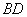 ⊥
⊥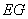 ;
;
(2)求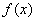 的最大值;
的最大值;
(3)当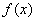 取得最大值时,求异面直线
取得最大值时,求异面直线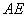 与
与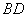 所成的角的余弦值.
所成的角的余弦值.
(法一)(1)证明:作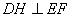 ,垂足
,垂足 ,连结
,连结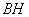 ,
, ,
,
∵平面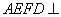 平面
平面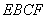 ,交线
,交线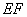 ,
,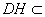 平面
平面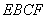 ,
,
∴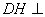 平面
平面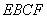 ,又
,又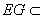 平面
平面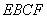 ,故
,故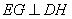 ,
,
∵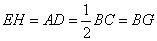 ,
,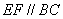 ,
,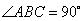 .
.
∴四边形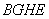 为正方形,故
为正方形,故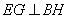 .
.
又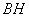 、
、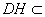 平面
平面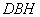 ,且
,且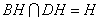 ,故
,故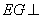 平面
平面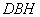 .
.
又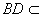 平面
平面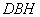 ,故
,故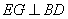 .
.
(2)解:∵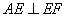 ,平面
,平面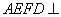 平面
平面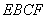 ,交线
,交线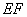 ,
,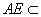 平面
平面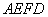 .
.
∴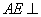 面
面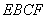 .又由(1)
.又由(1)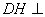 平面
平面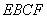 ,故
,故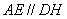 ,
,
∴四边形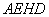 是矩形,
是矩形,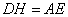 ,故以
,故以 、
、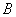 、
、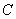 、
、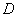 为顶点的三棱
为顶点的三棱
锥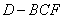 的高
的高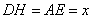 ,
,
又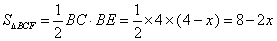 .
.
∴三棱锥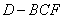 的体积
的体积
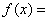
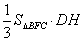
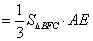
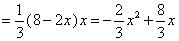
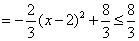 .
.
∴当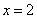 时,
时,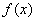 有最大值为
有最大值为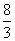 .
.
(3)解:由(2)知当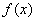 取得最大值时
取得最大值时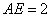 ,故
,故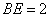 ,
,
由(2)知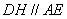 ,故
,故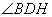 是异面直线
是异面直线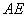 与
与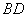 所成的角.
所成的角.
在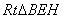 中
中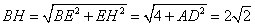 ,
,
由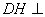 平面
平面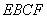 ,
,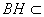 平面
平面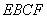 ,故
,故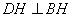
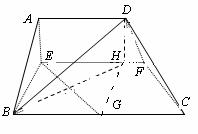 在
在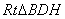 中
中
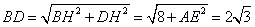 ,
,
∴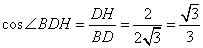 .
.
∴异面直线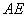 与
与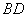 所成的角的余弦值为
所成的角的余弦值为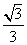 .
.
法二:(1)证明:∵平面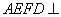 平面
平面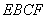 ,交线
,交线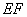 ,
,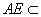 平面
平面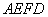 ,
,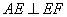 ,故
,故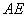 ⊥平面
⊥平面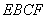 ,又
,又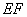 、
、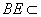 平面
平面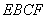 ,
,
∴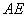 ⊥
⊥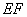 ,
,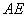 ⊥
⊥ ,又
,又 ⊥
⊥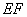 ,取
,取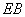 、
、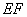 、
、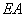 分别为
分别为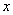 轴、
轴、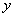
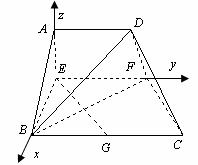
轴、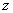 轴,建立空间坐标系
轴,建立空间坐标系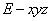 ,如图所示.
,如图所示.
当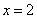 时,
时,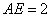 ,
,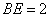 ,又
,又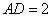 ,
,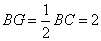 .
.
∴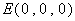 ,
,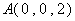 ,
,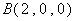 ,
,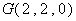 ,
,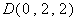 .
.
 ∴
∴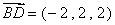 ,
,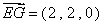 ,
,
∴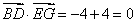 .
.
∴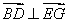 ,即
,即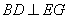 ;
;
(2)解:同法一;
(3)解:异面直线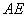 与
与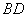 所成的角
所成的角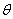 等于
等于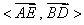 或其补角.
或其补角.
又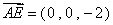 , 故
, 故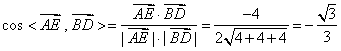
∴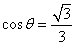 ,故异面直线
,故异面直线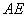 与
与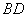 所成的角的余弦值为
所成的角的余弦值为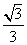 .
.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 (x2+2 x+1)dx=_________________
(x2+2 x+1)dx=_________________ ,
, ,
, ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( ) B.
B. C.
C. D.
D.
 中
中 ,
, ,则四边形
,则四边形 、
、 、
、 、
、 、
、 组成无重复数字的五位数,其中奇数有 个.
组成无重复数字的五位数,其中奇数有 个. 的解集是 ( )
的解集是 ( ) 1或x=-3} C.{x|x
1或x=-3} C.{x|x :
: ,若不等式
,若不等式 对任意实数
对任意实数 都成立,则实数
都成立,则实数 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
 在区间
在区间 单调递增,则满足
单调递增,则满足 <
< 的
的 取值范围是( )
取值范围是( )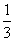 ,
, ) B. [
) B. [ ,
, 为不共线的三点,则“
为不共线的三点,则“ ”是“
”是“ 是钝角三角形”的
是钝角三角形”的