题目内容
已知:向量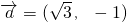 ,
, ,cos2x),(0<x<π),函数
,cos2x),(0<x<π),函数 .
.
(1)若f(x)=0,求x的值;
(2)求函数f(x)的取得最大值时,向量 与
与 的夹角.
的夹角.
解:∵ =
=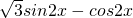
(1)由f(x)=0得 即
即
∵0<x<π,∴0<2x<2π
∴ ,或
,或 ,
,
∴ 或
或
(2)∵
= =
=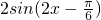
∴当 时,f(x)max=2
时,f(x)max=2
由上可得f(x)max=2,当f(x)=2时,
由 得
得 ,
,
∵ ∴
∴
分析:(1)根据两向量的坐标,利用向量积的计算求得函数f(x)的解析式,利用f(0)=0求得tan2x的值,进而x的范围求得x的值.
(2)利用两角和公式对函数解析式化简整理,然后利用正弦函数的性质求得函数的最大和最小值,最后利用向量的数量积的运算求得 与
与 的夹角的余弦值,进而求得其夹角.
的夹角的余弦值,进而求得其夹角.
点评:本题主要考查了三角函数的化简求值,二倍角公式的化简求值,向量数量积的运算.考查了基础知识的综合运用.
 =
=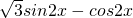
(1)由f(x)=0得
 即
即
∵0<x<π,∴0<2x<2π
∴
 ,或
,或 ,
,∴
 或
或
(2)∵

=
 =
=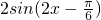
∴当
 时,f(x)max=2
时,f(x)max=2由上可得f(x)max=2,当f(x)=2时,
由
 得
得 ,
,∵
 ∴
∴
分析:(1)根据两向量的坐标,利用向量积的计算求得函数f(x)的解析式,利用f(0)=0求得tan2x的值,进而x的范围求得x的值.
(2)利用两角和公式对函数解析式化简整理,然后利用正弦函数的性质求得函数的最大和最小值,最后利用向量的数量积的运算求得
 与
与 的夹角的余弦值,进而求得其夹角.
的夹角的余弦值,进而求得其夹角.点评:本题主要考查了三角函数的化简求值,二倍角公式的化简求值,向量数量积的运算.考查了基础知识的综合运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目