题目内容
函数y=
sin2x+cos2x的最小正周期为 .
| 1 |
| 2 |
考点:三角函数的周期性及其求法
专题:计算题,三角函数的图像与性质
分析:根据二倍角的三角函数公式和两角和的正弦公式将函数表达式化简得y=
sin(2x+
)+
,再由三角函数的周期公式即可算出函数y的最小正周期.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
解答:
解:y=
sin2x+cos2x
=
sin2x+
=
sin(2x+
)+
∴函数f(x)的最小正周期T=
=π;
故答案为π.
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1+cos2x |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴函数f(x)的最小正周期T=
| 2π |
| 2 |
故答案为π.
点评:本题给出三角函数表达式,求它的最小正周期,着重考查了三角恒等变换公式和三角函数的图象与性质等知识点,属于中档题.

练习册系列答案
相关题目
已知命题p:复数z=
在复平面内所对应的点位于第四象限;命题q:?x>0使得2-x=ex,则下列命题中为真命题的是( )
| 1+i |
| i |
| A、p∧q |
| B、(¬p)∧q |
| C、p∧(¬q) |
| D、(¬p)∧(¬q) |
已知数列{an}满足:a1=1,
=
,n∈N*,{an}的前项和为Sn,则( )
| 1 |
| an+1 |
| 1 |
| 2an |
A、Sn=2-(
| ||
B、Sn=2-(
| ||
| C、Sn=2n-1 | ||
| D、Sn=2n-1-1 |
已知函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心为M(x0,y0),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0.若函数f(x)=x3-3x2,则可求出f(
)+f(
)+f(
)+…+f(
)+f(
)的值为( )
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4028 |
| 2015 |
| 4029 |
| 2015 |
| A、4029 | B、-4029 |
| C、8058 | D、-8058 |
“0<k<9”是“曲线
-
=1与曲线
-
=1的焦距相同”的( )
| x2 |
| 25 |
| y2 |
| 9-k |
| x2 |
| 25-k |
| y2 |
| 9 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
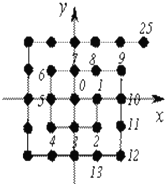 将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )
将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )| A、(1008,1007) |
| B、(1007,1006) |
| C、(1007,1005) |
| D、(1006,1005) |
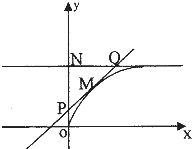 如图为函数f(x)=
如图为函数f(x)=