题目内容
设函数f(x)=ln x+ x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数).
(1)讨论f(x)的单调性;
(2)若a=1,证明:当x>1时,f(x)< x2-
x2-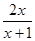 -
-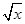 .
.
 x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数).(1)讨论f(x)的单调性;
(2)若a=1,证明:当x>1时,f(x)<
 x2-
x2-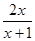 -
-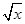 .
.(1) 在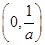 ,(1,+∞)上单调递增,在
,(1,+∞)上单调递增,在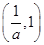 上单调递减(2)见解析
上单调递减(2)见解析
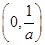 ,(1,+∞)上单调递增,在
,(1,+∞)上单调递增,在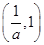 上单调递减(2)见解析
上单调递减(2)见解析(1)f(x)的定义域为(0,+∞),f′(x)=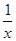 +ax-(a+1)=
+ax-(a+1)=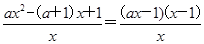 .
.
当0<a<1时,由f′(x)>0解得0<x<1或x>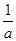 ,由f′(x)<0解得1<x<
,由f′(x)<0解得1<x<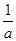 ,
,
所以函数f(x)在(0,1),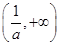 上单调递增,在
上单调递增,在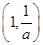 上单调递减.
上单调递减.
当a=1时,f′(x)≥0对x>0恒成立,所以函数f(x)在(0,+∞)上单调递增.
当a>1时,由f′(x)>0解得x>1或0<x<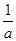 ,由f′(x)<0解得
,由f′(x)<0解得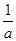 <x<1.
<x<1.
所以函数f(x)在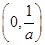 ,(1,+∞)上单调递增,在
,(1,+∞)上单调递增,在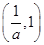 上单调递减.
上单调递减.
(2)证明:当a=1时,原不等式等价于ln x-2x+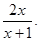 +
+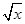 <0.
<0.
因为x>1,所以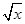 =
=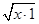 <
<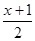 ,
,
因此ln x-2x+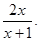 +
+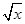 <ln x-2x+
<ln x-2x+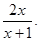 +
+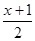 .
.
令g(x)=ln x-2x+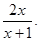 +
+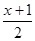 ,
,
则g′(x)=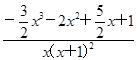 .
.
令h(x)=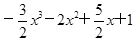 ,当x>1时,h′(x)=-
,当x>1时,h′(x)=-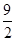 x2-4x+
x2-4x+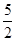 <0,
<0,
所以h(x)在(1,+∞)上单调递减,从而h(x)<h(1)=0,即g′(x)<0,
所以g(x)在(1,+∞)上单调递减,则g(x)<g(1)=0,
所以当x>1时,f(x)< x2-
x2-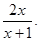 -
-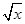 .
.
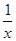 +ax-(a+1)=
+ax-(a+1)=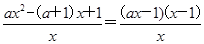 .
.当0<a<1时,由f′(x)>0解得0<x<1或x>
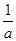 ,由f′(x)<0解得1<x<
,由f′(x)<0解得1<x<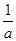 ,
,所以函数f(x)在(0,1),
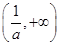 上单调递增,在
上单调递增,在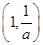 上单调递减.
上单调递减.当a=1时,f′(x)≥0对x>0恒成立,所以函数f(x)在(0,+∞)上单调递增.
当a>1时,由f′(x)>0解得x>1或0<x<
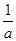 ,由f′(x)<0解得
,由f′(x)<0解得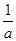 <x<1.
<x<1.所以函数f(x)在
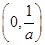 ,(1,+∞)上单调递增,在
,(1,+∞)上单调递增,在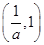 上单调递减.
上单调递减.(2)证明:当a=1时,原不等式等价于ln x-2x+
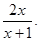 +
+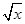 <0.
<0.因为x>1,所以
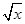 =
=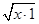 <
<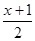 ,
,因此ln x-2x+
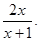 +
+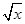 <ln x-2x+
<ln x-2x+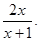 +
+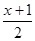 .
.令g(x)=ln x-2x+
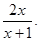 +
+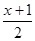 ,
,则g′(x)=
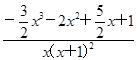 .
.令h(x)=
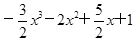 ,当x>1时,h′(x)=-
,当x>1时,h′(x)=-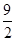 x2-4x+
x2-4x+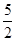 <0,
<0,所以h(x)在(1,+∞)上单调递减,从而h(x)<h(1)=0,即g′(x)<0,
所以g(x)在(1,+∞)上单调递减,则g(x)<g(1)=0,
所以当x>1时,f(x)<
 x2-
x2-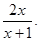 -
-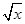 .
.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
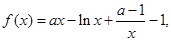 试讨论
试讨论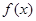 的单调性.
的单调性.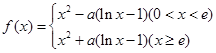 ,其中
,其中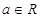 .
.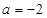 时,求函数
时,求函数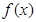 在区间
在区间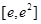 上的最大值;
上的最大值;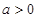 时,若
时,若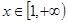 ,
,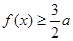 恒成立,求
恒成立,求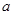 的取值范围.
的取值范围.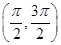
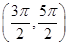
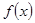 =
=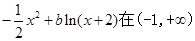 上是减函数,则
上是减函数,则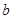 的取值范围是 。
的取值范围是 。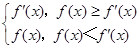 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.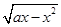 (a>0)的单调递减区间是________.
(a>0)的单调递减区间是________.