题目内容
若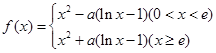 ,其中
,其中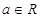 .
.
(1)当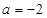 时,求函数
时,求函数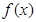 在区间
在区间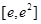 上的最大值;
上的最大值;
(2)当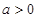 时,若
时,若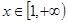 ,
,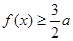 恒成立,求
恒成立,求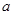 的取值范围.
的取值范围.
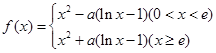 ,其中
,其中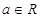 .
.(1)当
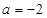 时,求函数
时,求函数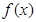 在区间
在区间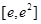 上的最大值;
上的最大值;(2)当
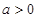 时,若
时,若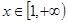 ,
,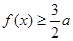 恒成立,求
恒成立,求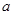 的取值范围.
的取值范围.(1)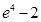 (2)
(2)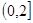
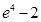 (2)
(2)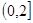
(1)当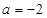 ,
,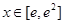 时,
时,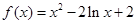 , (1分)
, (1分)
∵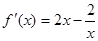 ,∴当
,∴当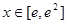 时,
时,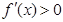 ,(2分)
,(2分)
∴函数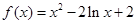 在
在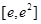 上单调递增, (3分)
上单调递增, (3分)
故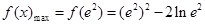
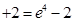 (4分)
(4分)
(2)①当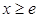 时,
时,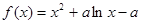 ,
,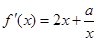 ,
,
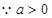 ,
,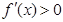 ,∴f(x)在
,∴f(x)在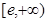 上增函数,(5分)
上增函数,(5分)
故当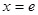 时,
时,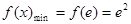 ;(6分)
;(6分)
②当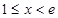 时,
时,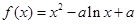 ,
,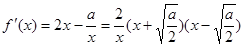 ,(7分)
,(7分)
(i)当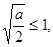 即
即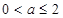 时,
时,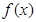 在区间
在区间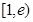 上为增函数,
上为增函数,
当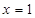 时,
时,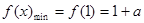 ,且此时
,且此时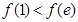
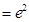 ;(8分)
;(8分)
(ii)当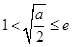 ,即
,即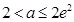 时,
时,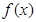 在区间
在区间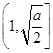 上为减函数,在区间
上为减函数,在区间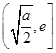 上为增函数,
上为增函数,
故当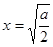 时,
时, ,且此时
,且此时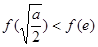
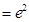 ;(10分)
;(10分)
(iii)当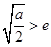 ,即
,即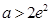 时,
时,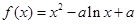 在区间[1,e]上为减函数,
在区间[1,e]上为减函数,
故当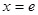 时,
时,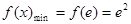 .(11分)
.(11分)
综上所述,函数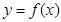 的在
的在 上的最小值为
上的最小值为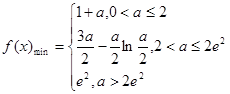 (12分)
(12分)
由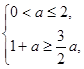 得
得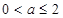 ;由
;由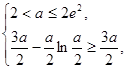 得无解;
得无解;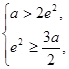 得无解;(13分)
得无解;(13分)
故所求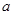 的取值范围是
的取值范围是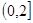 .
.
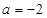 ,
,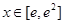 时,
时,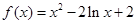 , (1分)
, (1分)∵
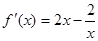 ,∴当
,∴当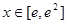 时,
时,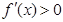 ,(2分)
,(2分)∴函数
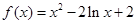 在
在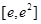 上单调递增, (3分)
上单调递增, (3分)故
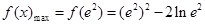
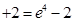 (4分)
(4分)(2)①当
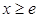 时,
时,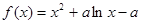 ,
,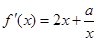 ,
,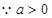 ,
,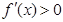 ,∴f(x)在
,∴f(x)在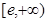 上增函数,(5分)
上增函数,(5分)故当
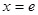 时,
时,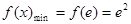 ;(6分)
;(6分)②当
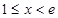 时,
时,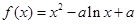 ,
,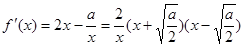 ,(7分)
,(7分)(i)当
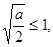 即
即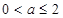 时,
时,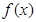 在区间
在区间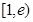 上为增函数,
上为增函数,当
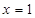 时,
时,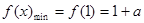 ,且此时
,且此时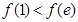
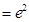 ;(8分)
;(8分)(ii)当
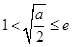 ,即
,即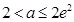 时,
时,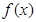 在区间
在区间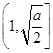 上为减函数,在区间
上为减函数,在区间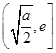 上为增函数,
上为增函数,故当
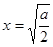 时,
时, ,且此时
,且此时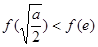
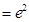 ;(10分)
;(10分)(iii)当
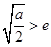 ,即
,即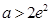 时,
时,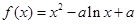 在区间[1,e]上为减函数,
在区间[1,e]上为减函数,故当
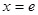 时,
时,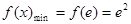 .(11分)
.(11分)综上所述,函数
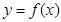 的在
的在 上的最小值为
上的最小值为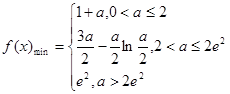 (12分)
(12分)由
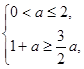 得
得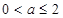 ;由
;由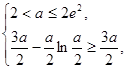 得无解;
得无解;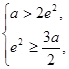 得无解;(13分)
得无解;(13分)故所求
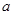 的取值范围是
的取值范围是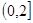 .
.
练习册系列答案
相关题目
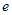 是自然对数的底数,函数
是自然对数的底数,函数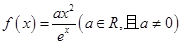 。
。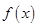 的单调递增区间;
的单调递增区间;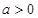 时,函数
时,函数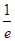 ,求
,求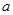 的值。
的值。 x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数). x2-
x2-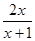 -
-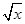 .
.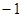 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .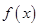 在R上可导,其导函数
在R上可导,其导函数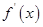 ,且函数
,且函数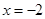 处取得极小值,则函数
处取得极小值,则函数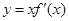 的图像可能是( )
的图像可能是( )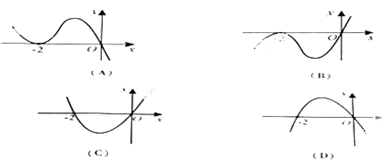
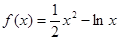 的单调递减区间为( )
的单调递减区间为( ) 1,1)
1,1)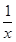 在
在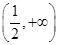 上是增函数,则a的取值范围是________.
上是增函数,则a的取值范围是________.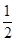 x2+blnx在区间[
x2+blnx在区间[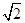 ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.