题目内容
11.已知a,b为互不相等的正数,试比较ab(a+b)+bc(b+c)+ac(a+c)与6abc的大小ab(a+b)+bc(b+c)+ac(a+c)>6abc.分析 a,b为互不相等的正数,利用基本不等式的性质可得:a2b+bc2>2abc,ab2+ac2>2abc,b2c+a2c>2abc,即可得出.
解答 解:∵a,b为互不相等的正数,
∴a2b+bc2>2abc,
ab2+ac2>2abc,
b2c+a2c>2abc,
∴a2b+bc2+ab2+ac2+b2c+a2c>6abc,
∴ab(a+b)+bc(b+c)+ac(a+c)-6abc>0,
故答案为:ab(a+b)+bc(b+c)+ac(a+c)-6abc>0.
点评 本题考查了基本不等式的解法、作差法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.如图所示,双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,M,N为双曲线C上两点,且kMN=0,若$\overrightarrow{{F}_{1}Q}$=$\overrightarrow{QN}$(Q在双曲线C上),且|MN|=$\frac{{|F}_{1}{F}_{2}|}{4}$,则双曲线C的渐近线方程为( )
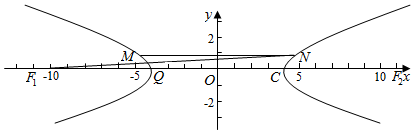
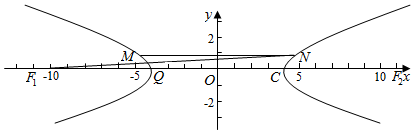
| A. | y=$±\sqrt{2}$x | B. | y=$±\sqrt{3}$x | C. | y=±2x | D. | y=$±\sqrt{5}$x |
16.过直线x+y=2与x-y=0的交点,且法向量为$\overrightarrow{n}$=(2,-3)的直线方程是( )
| A. | -3x+2y+1=0 | B. | 3x-2y+1=0 | C. | -2x+3y+1=0 | D. | 2x-3y+1=0 |