题目内容
已知数列 是等差数列,首项
是等差数列,首项 ,公差为
,公差为 ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)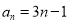 ;(2)
;(2)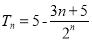 .
.
【解析】
试题分析:(1)在等差数列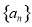 中,知道首项,再利用等比中项的性质得到
中,知道首项,再利用等比中项的性质得到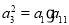 ,利用等差数列的公式转化为首项和公差表示,进而联立求得
,利用等差数列的公式转化为首项和公差表示,进而联立求得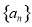 中的首项和公差,求得其通项公式
中的首项和公差,求得其通项公式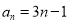 ;(2)根据(1)得到数列
;(2)根据(1)得到数列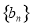 的通项公式,
的通项公式,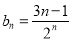 ,再利用错位相减法求得
,再利用错位相减法求得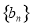 的前
的前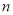 项和
项和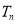 .
.
试题解析:(1)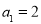 ,设公差为
,设公差为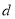 ,则由
,则由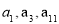 成等比数列,
成等比数列,
得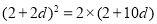 ,
,
解得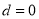 (舍去)或
(舍去)或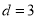 ,
,
所以数列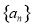 的通项公式为
的通项公式为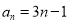
(2)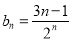 ,
,
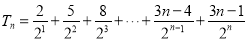
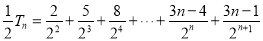
-得: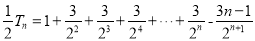

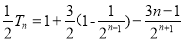
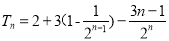
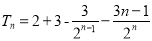
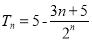
考点:1.等差数列公式;2.错位相减法求和.

练习册系列答案
相关题目
 ,
, ,则
,则 的最小值是 .
的最小值是 .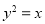 的焦点,点A,B在该抛物线上且位于x轴的两侧,
的焦点,点A,B在该抛物线上且位于x轴的两侧,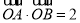 (其中O为坐标原点),则△AFO与△BFO面积之和的最小值是( )
(其中O为坐标原点),则△AFO与△BFO面积之和的最小值是( )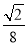 B.
B.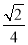 C.
C.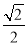 D.
D.
 ,这两个球相外切,且球
,这两个球相外切,且球  与正方体共顶点A的三个面相切,球
与正方体共顶点A的三个面相切,球  与正方体共顶点
与正方体共顶点  的三个面相切,则两球在正方体的面
的三个面相切,则两球在正方体的面  上的正投影是( )
上的正投影是( )

 是等差数列,若
是等差数列,若  ,则
,则  等于( )
等于( ) 的样本的重量频率分布直方图,则由图可估计样本重量的中位数为 .
的样本的重量频率分布直方图,则由图可估计样本重量的中位数为 .
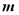 和
和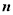 的夹角为
的夹角为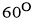 ,记
,记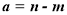 ,
, 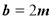 , 则向量
, 则向量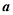 与
与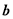 的夹角为 ( )
的夹角为 ( )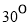 (B)
(B)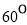 (C)
(C)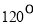 (D)
(D)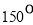
 是虚数单位,则
是虚数单位,则 .
. ,则该几何体的体积为 .
,则该几何体的体积为 .