题目内容
对于函数f（x）=ax2+bx+
-1．
（1）当a=1，b=-2时，求函数f（x）的零点；
（2）若对任意实数b，函数f（x）恒有两个相异的零点，求实数a的取值范围．
| b |
| a |
（1）当a=1，b=-2时，求函数f（x）的零点；
（2）若对任意实数b，函数f（x）恒有两个相异的零点，求实数a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）把所给的数字代入解析式，得到函数的解析式，要求函数的零点，只要使函数等于0就可以，解一元二次方程，得到结果．
（2）函数恒成立问题，首先函数恒有两个相异的零点，得到函数的判别式大于0，对于b的值，不管b取什么，都能够使得不等式成立，注意再次使用函数的判别式．
（2）函数恒成立问题，首先函数恒有两个相异的零点，得到函数的判别式大于0，对于b的值，不管b取什么，都能够使得不等式成立，注意再次使用函数的判别式．
解答：
解：（1）当a=1，b=-2时，f（x）=x2-2x-3．
由f（x）=x2-2x-3=0，
解得x1=-1，x2=3
∴函数f（x）的零点为-1，3．
（2）∵对任意实数b，函数f（x）恒有两个相异的零点，
∴a≠0，且△=b2-4b+4a＞0对于b∈R恒成立，
∴△′=16-16a＜0，解得a＞1．
∴实数a的取值范围是（1，+∞）．
由f（x）=x2-2x-3=0，
解得x1=-1，x2=3
∴函数f（x）的零点为-1，3．
（2）∵对任意实数b，函数f（x）恒有两个相异的零点，
∴a≠0，且△=b2-4b+4a＞0对于b∈R恒成立，
∴△′=16-16a＜0，解得a＞1．
∴实数a的取值范围是（1，+∞）．
点评：本题考查函数的零点的判定，在第二问中，注意两次使用函数的判别式，这是函数的综合题目中常见的一种题型．
练习册系列答案
相关题目
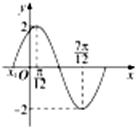已知函数f（x）=Asin（ωx+φ）在一个周期内的图象如图所示．
平行四边形ABCD中，BC=2，CD=