题目内容
在平面直角坐标系中,有A、B两个点,其中A(-6,3)、B(-2,5).
(1)若一只青蛙从A点跳到x轴上一点P处,再从P点跳到B点,则青蛙所跳的路程最短时点P的坐标是 .
(2)若这只青蛙先从A点出发跳到B点,再从B点跳到y轴上的C点,继续从C点跳到x轴上的D点,最后从D点回到A点(青蛙每次所跳的距离不一定相等),当青蛙四步跳完的路程最短时,直线CD的解析式是 .
(1)若一只青蛙从A点跳到x轴上一点P处,再从P点跳到B点,则青蛙所跳的路程最短时点P的坐标是
(2)若这只青蛙先从A点出发跳到B点,再从B点跳到y轴上的C点,继续从C点跳到x轴上的D点,最后从D点回到A点(青蛙每次所跳的距离不一定相等),当青蛙四步跳完的路程最短时,直线CD的解析式是
考点:进行简单的合情推理
专题:计算题,作图题,推理和证明
分析:作图,(1)|AP|+|BP|=|A'P|+|BP|≥|AB|,当A'PB三点共线时,|AP|+|BP|最小;
(2)同理当A',C,D,B'四点共线时,青蛙四步跳完的路程最短,从而求直线CD的解析式.
(2)同理当A',C,D,B'四点共线时,青蛙四步跳完的路程最短,从而求直线CD的解析式.
解答:
 解:如右图:
解:如右图:
(1)|AP|+|BP|=|A'P|+|BP|≥|AB|,
当A'PB三点共线时,|AP|+|BP|最小,
此时点P是直线A'B与x轴的交点,
直线A'B的方程为y-5=
(x+2),
令y=0得,x=-4.5,即点P的坐标为(-4.5,0).
(2)同(1),当A',C,D,B'四点共线时,青蛙四步跳完的路程最短,
直线CD的解析式是
=
,
即y=x+3.
故答案为:(-4.5,0),y=x+3.
 解:如右图:
解:如右图:(1)|AP|+|BP|=|A'P|+|BP|≥|AB|,
当A'PB三点共线时,|AP|+|BP|最小,
此时点P是直线A'B与x轴的交点,
直线A'B的方程为y-5=
| 5+3 |
| -2+6 |
令y=0得,x=-4.5,即点P的坐标为(-4.5,0).
(2)同(1),当A',C,D,B'四点共线时,青蛙四步跳完的路程最短,
直线CD的解析式是
| y+3 |
| 5+3 |
| x+6 |
| 2+6 |
即y=x+3.
故答案为:(-4.5,0),y=x+3.
点评:本题考查了学生的作图能力及实际问题化为数学问题的能力,属于中档题.

练习册系列答案
相关题目
已知a=log23,则用a的代数式表示log38-log26=( )
A、
| ||
| B、2a-1 | ||
C、
| ||
| D、4a-1 |
若集合M={0,1},N={1,2},则M∪N等于( )
| A、{1} |
| B、{0,1} |
| C、{1,2} |
| D、{0,1,2} |
经过两点A(-2,0)、B(-5,3)的直线的斜率是( )
A、
| ||
| B、-1 | ||
C、
| ||
| D、1 |
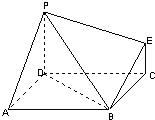 如图为一简单几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.