Question

设f(x)=ax²+bx+c(a≠0),如果对任意x∈［-1,1］,都有|f(x)|≤1,试证对任意x∈［-1,1］均有|2ax+b|≤4.

Answer 1

证明：设g(x)=2ax+b,则g(x)为单调函数.故只需证|g(1)|≤4,且|g(-1)|≤4.

由于对任意x∈［-1,1］,均有-1≤f(x)≤1,

∴

∴

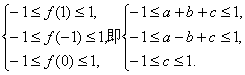
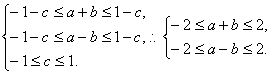
∴-2≤a≤2.

又∵2a±b=a+(a±b),∴-4≤2a±b≤4,

即-4≤g(±1)≤4,即|g(±1)|≤4.

∴对任意x∈［-1,1］,均有|2ax+b|≤4.