题目内容
已知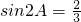
，A∈（0，π），则sinA+cosA=
- A.
- B.
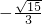
- C.
- D.
A
分析：根据sin2A=2sinAcosA，A∈（0，π），可确定角A的范围，再对sinA+cosA进行平方可得答案．
解答：由sin2A=2sinAcosA=
＞0，又A∈（0，π）．
所以A∈（0，
），所以sinA+cosA＞0
又（sinA+cosA）2=1+2sinAcosA=
故选A．
点评：本题主要考查三角函数的二倍角公式的应用．注意角的取值范围给结果带来的影响．
分析：根据sin2A=2sinAcosA，A∈（0，π），可确定角A的范围，再对sinA+cosA进行平方可得答案．
解答：由sin2A=2sinAcosA=
＞0，又A∈（0，π）．所以A∈（0，
），所以sinA+cosA＞0又（sinA+cosA）2=1+2sinAcosA=
故选A．
点评：本题主要考查三角函数的二倍角公式的应用．注意角的取值范围给结果带来的影响．
练习册系列答案
相关题目
在一条东西走向的水平公路的北侧远处有一座高塔，塔底与这条公路在同一水平面上，为了测量该塔的高度，测量人员在公路上选择了A、B两个观测点，在A处测得该塔底部C在西偏北α的方向上，在B处测得塔底C在西偏北β的方向上，并测得塔顶D的仰角为γ，已知AB=a，0＜γ＜β＜α＜
，则此塔高CD为（ ）
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|