题目内容

已知点A（0，0），B(
3
，0)，C（0，1）．设AD⊥BC于D，那么有
CD
=λ
CB
，其中λ=
 
．
分析：由A，B，C三点的坐标，及AD⊥BC于D，由射影定理我们不难求出线段CD，与CB的长度，由图分析，向量
CD
与
CB
同向，故λ＞0；综合可得答案．
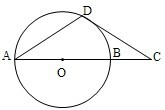
解答：精英家教网解：已知如图，A、B、C、D四点坐标如下图示：
由射影定理，可得：CD=
1
2
，CB=2
由
CD
与
CB
同向
∴
CD
=
1
4
CB

故λ=
1
4

故答案为：
1
4
点评：若向量
a
与非零向量
b
满足，
a
=λ
b
，则：
当λ＞0时，向量
a
与微量
b
同向，且λ=
|
a
|
|
b
|
，
当λ=0时，向量
a
=
0
，
当λ＜0时，向量
a
与微量
b
反向，且λ=-
|
a
|
|
b
|
．
练习册系列答案
相关题目
精英家教网本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A：AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC．
B：在平面直角坐标系xOy中，已知点A（0，0），B（-2，0），C（-2，1）．设k为非零实数，矩阵M=
k0
01
，N=
01
10
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，求k的值．
C：在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切，求实数a的值．
D：设a、b是非负实数，求证：a3+b3≥
ab
(a2+b2)．
（1）选修4-2：矩阵与变换
在平面直角坐标系xOy中，已知点A（0，0），B（-2，0），C（-2，1）．设k为非零实数，矩阵M=
k0
01
，N=
01
10
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，求k的值．
在平面直角坐标系xOy中，已知点A（0，0），B（-2，0），C（-2，1）．设k为非零实数，矩阵M=
.
k0
01
.
，N=
.
01
10
.
，点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1，△A1B1C1的面积是△ABC面积的2倍，
（1）求k的值．
（2）判断变换MN是否可逆，如果可逆，求矩阵MN的逆矩阵；如不可逆，说明理由．
在平面直角坐标系xOy中，已知点A（0，2）、B（1，1），直线 l经过点B且与线段OA相交．则直线 l倾斜角α的取值范围是
[0，
π
4
]∪[
3π
4
，π)
[0，
π
4
]∪[
3π
4
，π)
．
已知点A（-2，0），B（2，0），直线AG，BG相交于点G，且它们的斜率之积是-
14
．
（Ⅰ）求点G的轨迹Ω的方程；
（Ⅱ）圆x2+y2=4上有一个动点P，且P在x轴的上方，点C（1，0），直线PA交（Ⅰ）中的轨迹Ω于D，连接PB，CD．设直线PB，CD的斜率存在且分别为k1，k2，若k1=λk2，求实数λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网