题目内容
20．设正方体ABCD-A1B1C1D1的棱长为a，则有（ ）| A． | $\overrightarrow{AB}$•$\overrightarrow{{A}_{1}{C}_{1}}$=a2 | B． | $\overrightarrow{A{C}_{1}}$•$\overrightarrow{B{D}_{1}}$=0 | C． | $\overrightarrow{AB}$•$\overrightarrow{A{C}_{1}}$=$\sqrt{2}$a2 | D． | $\overrightarrow{BC}$•$\overrightarrow{D{A}_{1}}$=a2 |
分析 建立空间直角坐标系，求出各向量的坐标，代入数量积公式计算．
解答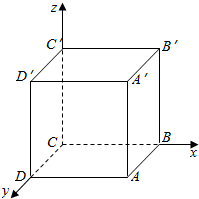 
解：建立如图所示的空间坐标系，则A（a，a，0），B（a，0，0），C（0，0，0），D（0，a，0），A1（a，a，a），C1（0，0，a），D1（0，a，a）．
$\overrightarrow{AB}$=（0，-a，0），$\overrightarrow{A{{\;}_{1}C}_{1}}$=（-a，-a，0），$\overrightarrow{A{C}_{1}}$=（-a，-a，a），$\overrightarrow{B{D}_{1}}$=（-a，a，a），$\overrightarrow{BC}$=（-a，0，0），$\overrightarrow{D{A}_{1}}$=（a，0，a）．
∴$\overrightarrow{AB}•\overrightarrow{{A}_{1}{C}_{1}}$=a2，$\overrightarrow{A{C}_{1}}•\overrightarrow{B{D}_{1}}$=a2，$\overrightarrow{AB}•\overrightarrow{A{C}_{1}}$=a2，$\overrightarrow{BC}•\overrightarrow{D{A}_{1}}$=-a2．
故选：A．
点评 本题考查了平面向量的数量积运算，建立空间坐标系可使计算简单，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
10．复数z=i（1+i）（i是虚数单位）在复平面内所对应点的坐标为（ ）
| A． | （1，1） | B． | （-1，-1） | C． | （1，-1） | D． | （-1，1） |
11．下列函数中，为偶函数的是（ ）
| A． | $y=\sqrt{x}$ | B． | y=2x | C． | y=sinx | D． | y=cosx |
8．将函数f（x）=2sin（2x-$\frac{π}{3}$）的图象向左平移$\frac{π}{4}$个单位，得到函数g（x）的图象，则函数g（x）的一个单调递减区间是（ ）
| A． | [-$\frac{5π}{12}$，0] | B． | [-$\frac{π}{3}$，0] | C． | [0，$\frac{π}{3}$] | D． | [$\frac{π}{6}$，$\frac{π}{2}$] |
9．已知A（4，0）、B（0，5）是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两个顶点，C是椭圆上处于第一象限内的点，则△ABC面积的最大值为（ ）
| A． | 10（$\sqrt{3}$-1） | B． | 10（$\sqrt{2}$+1） | C． | 10（$\sqrt{2}$-1） | D． | 10（$\sqrt{3}$+1） |
如图，已知点F（1，0），点A，B分别在x轴、y轴上运动，且满足AB⊥BF，$\overrightarrow{AD}$=2$\overrightarrow{AB}$，设点D的轨迹为C．