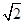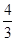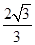题目内容
已知双曲线
-
=1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
-=1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )A． | B． |
C． | D． |
D
由题意知三角形OMN为等腰直角三角形,
所以|MF|=|OF|=c,所以点M(c,c),
当x=c时,
-=1,得|y|=
,
所以由|y|==c得b2=ac,
即c2-a2=ac,c2-ac-a2=0,
所以e2-e-1=0,
解得离心率e=.故选D.
所以|MF|=|OF|=c,所以点M(c,c),
当x=c时,
-=1,得|y|=,所以由|y|=
=c得b2=ac,即c2-a2=ac,c2-ac-a2=0,
所以e2-e-1=0,
解得离心率e=
.故选D.
练习册系列答案
相关题目
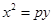的焦点与双曲线
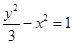的上焦点重合，则p的值为 
-
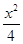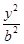=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等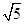
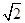
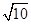,0),B(
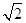的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )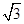
-
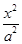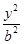=1(a>0,b>0),离心率e=
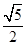,顶点到渐近线的距离为
.
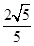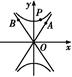
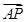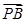=λ
,λ∈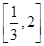
.求△AOB的面积的取值范围.
-
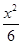=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )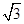
-
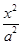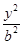=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
-
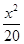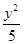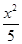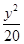=1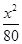
-
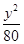=1
-
=1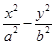
＝1(a＞0，b＞0)的右焦点为F，过点F作一条渐近线的垂线，垂足为A，△OAF的面积为
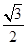a2(O为原点)，则此双曲线的离心率是( )
