题目内容
8.函数f(x)=1g[(1-a2)x2+3(1-a)x+6]值域为R,则实数a的取值范围是( )| A. | (-1,0) | B. | (-1,-$\frac{5}{11}$) | C. | [-1,-$\frac{5}{11}$) | D. | [-1,-$\frac{5}{11}$] |
分析 本题对函数中x2项的系数进行分类讨论,确保内函数的值能够取到每一个正数.
解答 解:∵函数f(x)=lg[(1-a2)x2+3(1-a)x+6]的值域为R,
∴当a-1=0时,a=1,
lg[(1-a2)x2+3(1-a)x+6]=lg6;
当a=-1时,f(x)=lg(6x+6),x>-1时,f(x)的值域是R,
对于方程(1-a2)x2+3(1-a)x+6=0,
二次项系数1-a2>0,
根的判别式△=9(1-a)2-24(1-a2)≥0,
∴-1≤a≤-$\frac{5}{11}$.
故选:D.
点评 本题考查了函数的值域,还考查了分类讨论的数学思想,本题难度不大,属于中档题.

练习册系列答案
相关题目
18.已知映射f:x→lgx+1,则像2在f作用下的原像为( )
| A. | lg2+1 | B. | 1 | C. | 10 | D. | 100 |
16.函数f(x)=lo${g}_{\frac{1}{2}}$(x2-ax)在区间[2,4]上是减函数,则实数a的取值范围是( )
| A. | 2<a≤4 | B. | a≤4 | C. | a<2 | D. | a≤2 |
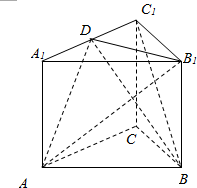 如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧楞长为$\sqrt{2}$,D为A1C1中点.
如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧楞长为$\sqrt{2}$,D为A1C1中点.