Question

15．已知函数f（x）=$\frac{|x|+1}{|x+1|}$，
（1）画出该函数的图象；
（2）写出它的定义域，单调区间，奇偶性，值域；
（3）若方程a=$\frac{|x|+1}{|x+1|}$有两个实根，求出实数a的取值范围．

Answer 1

分析 （1）化为分段函数，再画图即可，
（2）由图象可求它的定义域，单调区间，奇偶性，值域，
（3）方程a=$\frac{|x|+1}{|x+1|}$有两个实根转化为则y=a，与y=f（x）有两个交点，又图象可知a的范围．

解答 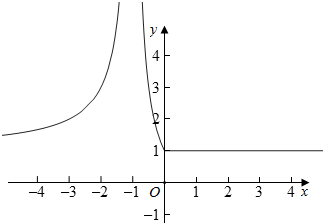解：（1）f（x）=$\frac{|x|+1}{|x+1|}$=$\left\{\begin{array}{l}{1，x≥0}\\{\frac{2}{x+1}-1，-1＜x＜0}\\{-\frac{2}{x+1}+1，x＜-1}\end{array}\right.$，其图象如图所示：
（2）由图象可知，它的定义域为（-∞，-1）∪（-1，+∞），
f（x）在（-∞，-1）上为增函数，在（-1，0]上为减函数，
f（x）为非奇非偶函数，
f（x）值域为[1，+∞）；
（3）方程a=$\frac{|x|+1}{|x+1|}$有两个实根，
则y=a，与y=f（x）有两个交点，
由图象可知a＞1．

点评 本题考查了函数图象和画法和识别，关键是化为分段函数，属于基础题