题目内容
20.已知函数y=x2-lnx的一条切线是y=x-b,则b=0.分析 求函数的导数,利用导数的几何意义求出切线方程即可得到结论.
解答 解:函数的定义域为(0,+∞),导数f′(x)=2x-$\frac{1}{x}$,
若函数y=x2-lnx的一条切线是y=x-b,
则此切线斜率k=1,
由f′(x)=2x-$\frac{1}{x}$=1得2x2-x-1=0,得x=1或x=$-\frac{1}{2}$(舍),
当x=1时,y=1-ln1=1,即切点坐标为(1,1),
同时(1,1)也在y=x-b上,
∴1=1-b,则b=0,
故答案为:0
点评 本题主要考查导数的几何意义的应用,求出函数的导数,建立切线斜率相等的关系,进行求解是解决本题的关键.

练习册系列答案
相关题目
11.若实数x,y满足$\left\{\begin{array}{l}x+y-3≥0\\ x-y-3≤0\\ 0≤y≤1\end{array}\right.$,则$z=\frac{2x+y}{x+y}$的最小值为( )
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
8.已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若?x∈(0,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是( )
| A. | $({-∞,2\sqrt{2}})$ | B. | $({-∞,2\sqrt{2}}]$ | C. | $({0,2\sqrt{2}}]$ | D. | $({2\sqrt{2},+∞})$ |
15.已知函数f(x)的图象在点(x0,f(x0))处的切线方程l:y=g(x),若函数f(x)满足?x∈l(其中I为函数f(x)的定义域),当x≠x0时,[f(x)-g(x)](x-x0)>0恒成立,则称x0为函数f(x)的“转折点”,若函数f(x)=lnx-ax2-x在(0,e]上存在一个“转折点”,则a的取值范围为( )
| A. | $[{\frac{1}{{2{e^2}}},+∞})$ | B. | $({-1,\frac{1}{{2{e^2}}}}]$ | C. | $[{-\frac{1}{{2{e^2}}},1})$ | D. | $({-∞,-\frac{1}{{2{e^2}}}}]$ |
5.在平面直角坐标系xOy中,向量$\overrightarrow{OA}$=(-1,2),$\overrightarrow{OB}$=(2,m),若O,A,B三点能构成三角形,则( )
| A. | m=-4 | B. | m≠-4 | C. | m≠1 | D. | m∈R |
10.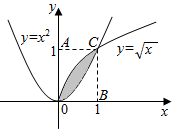 由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示,则图中阴影部分面积为( )
由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示,则图中阴影部分面积为( )
 由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示,则图中阴影部分面积为( )
由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示,则图中阴影部分面积为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |