题目内容
在直角坐标系xOy中，直线l的参数方程为
（t为参数，0≤α<π）。以原点为极点，x轴的正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
ρcos2θ=4sinθ。
（1）求直线l与曲线C的平面直角坐标方程；
（2）设直线l与曲线C交于不同的两点A、B，若
，求α的值。
（1）
（2）
或
解析试题分析：（1）先利用消去参数
得到曲线
的直角坐标方程．再将原极坐标方程
,两边同时乘以
，利用极坐标与直角坐标之间的关系即可得出其直角坐标方程；
（2）将代入曲线的标准方程：
得：
，利用直线的参数方程中的几何意义结合根与系数的关系建立关于
的方程即可求出求出的值．
试题解析：（1）直线
普通方程为
曲线的极坐标方程为
，则
5分
（2）将
代入曲线
7分
9分或 10分
考点：1.直线的参数方程；2.曲线的极坐标方程.
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
轴正半轴．已知曲线
的极坐标方程为
，曲线
的参数方程为
（其中
为参数）
的直角坐标方程和曲线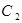
的普通方程；
的直线与圆
：
的一个交点为
，点
为线段
的中点。
，方向向量为
的直线，圆方程
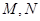两点，求
的值
(t为参数)相交于A、B两点，求|AB|.
，求|CP|.
到直线ρsinθ＝2的距离．
＝2
.
(t∈R为参数)，求a，b的值．