题目内容
【题目】已知数列{an}，{bn}满足：bn=an+1﹣an（n∈N*）．
（1）若a1=1，bn=n，求数列{an}的通项公式；
（2）若bn+1bn﹣1=bn（n≥2），且b1=1，b2=2． （i）记cn=a6n﹣1（n≥1），求证：数列{cn}为等差数列；
（ii）若数列{ 
}中任意一项的值均未在该数列中重复出现无数次，求首项a1应满足的条件．
【答案】
（1）解：当n≥2时，有an=a1+（a2﹣a1）+（a3﹣a2）++（an﹣an﹣1）
=a1+b1+b2++bn﹣1
= 
﹣ 
+1；
又a1=1也满足上式，所以数列{an}的通项公式是an= ﹣ +1
（2）解：（ i）因为对任意的n∈N*，有bn+6= 
= 
= 
=bn，
所以cn+1﹣cn=a6n+5﹣a6n﹣1
=b6n﹣1+b6n+b6n+1+b6n+2+b6n+3+b6n+4
=1+2+2+1+ 
+ =7，
所以，数列{cn}为等差数列；
（ ii）设cn=a6（n﹣1）+i（n∈N*）（其中i为常数且i∈{1，2，3，4，5，6}，
所以cn+1﹣cn=a6（n﹣1）+6+i﹣a6（n﹣1）+i
=b6（n﹣1）+i+b6（n﹣1）+i+1+b6（n﹣1）+i+2+b6（n﹣1）+i+3
+b6（n﹣1）+i+4+b6（n﹣1）+i+5=7，
即数列{a6（n﹣1）+i}均为以7为公差的等差数列；
设fk= 
= 
= 
= 
+ 
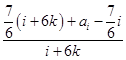（其中n=6k+i，k≥0，i为{1，2，3，4，5，6}中一个常数）
当ai= i时，对任意的n=6k+i，有 
= ；
当ai≠ i时，fk+1﹣fk=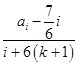 
﹣ =（ai﹣ i） 
①若ai＞ i，则对任意的k∈N有fk+1＜fk，所以数列{ }为递减数列
②若ai＜ i，则对任意的k∈N有fk+1＞fk，所以数列{ }为递增数列．
综上所述，集合B={ }∪{ 
}∪{ }∪{﹣ 
}∪{﹣ 
}={ ， ， ，﹣ ，﹣ }．
当a1∈B时，数列{ }中必有某数重复出现无数次；
当a1B时，数列{ }（i=1，2，3，4，5，6）均为单调数列，
任意一个数在这6个数列中最多出现一次，
所以数列{ }任意一项的值均未在该数列中重复出现无数次．
【解析】（1）根据递推数列求出数列{an}的通项公式；（2）（i）根据等差数列的定义，证明数列{cn}为等差数列；（ii）设cn=a6（n﹣1）+i（n∈N*），判断数列{a6（n﹣1+i}以7为公差的等差数列；
设fk= 
，计算fk+1﹣fk的值，求出a1满足的条件即可．
【考点精析】通过灵活运用等差关系的确定和数列的通项公式，掌握如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式即可以解答此题．
中考解读考点精练系列答案
