题目内容
【题目】已知椭圆E： 
+ 
=1（a＞b＞0）上点P，其左、右焦点分别为F1 ， F2 ， △PF1F2的面积的最大值为 
，且满足 
=3
（1）求椭圆E的方程；
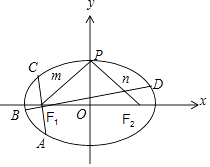
（2）若A，B，C，D是椭圆上互不重合的四个点，AC与BD相交于F1 ， 且 
=0，求 
的取值范围．
【答案】
（1）解：如图，设|PF1|=m，|PF2|=n，由 
=2，
得 
，即 
，
由△PF1F2的面积的最大值为 
，得bc= ．
联立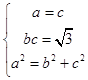 
，解得a=2，b= ．
∴椭圆E的方程为 
；
（2）解：当直线AC斜率不存在时， 
= 
，当直线AC斜率为0时， = 
，
当直线AC斜率存在且不为0时，设直线AC：y=k（x+1），A（x1，y1）C（x2，y2），BD： 
，
联立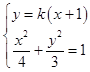 
，整理得（3+4k2）x2+8k2x+4k2﹣12=0，
∴ 
， 
，
则|AC|= 
= 
．
将 
代入上式可得|BD|= 
，
则 = 
，
由k2＞0，则 
，
综上， 的取值范围为[ ， ]．
【解析】（1）由已知可得关于a，b，c的方程组，求解方程组得到a，b的值，则椭圆方程可求．（2）设直线AC的方程，代入椭圆方程，利用韦达定理以及弦长公式即可求得|AC|的值，将 
代入上式可得|BD|，由k2＞0，即可求得 
的取值范围．
练习册系列答案
相关题目
