题目内容
17.设直线l过点M(1,1),倾斜角为$\frac{π}{6}$(1)写出直线l的参数方程;
(2)求直线l与直线l1:x-y-2$\sqrt{3}$=0的交点P的坐标及|PM|;
(3)已知直线l与圆C:x2+y2=4交于两点A、B,求:AB中点坐标.
分析 (1)设直线上任意一点到M的有向距离为t,得出该点的坐标,即为直线的参数方程;
(2)将直线l的参数方程代入直线l1的方程求出t,即为|PM|,将t代入参数方程求得P点坐标;
(3)联立直线l与圆C的方程消元,利用根与系数的关系和中点坐标公式求出中点坐标.
解答 解:(1)直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$(t为参数).
(2)将直线l的参数方程代入x-y-2$\sqrt{3}$=0得$\frac{\sqrt{3}}{2}t-\frac{1}{2}t-2\sqrt{3}=0$,
解得t=6+2$\sqrt{3}$.
∴x=1+$\frac{\sqrt{3}}{2}$(6+2$\sqrt{3}$)=4+3$\sqrt{3}$,y=1+$\frac{1}{2}$(6+2$\sqrt{3}$)=4+$\sqrt{3}$.
即P(4+3$\sqrt{3}$,4+$\sqrt{3}$).
∴|PM|=t=6+2$\sqrt{3}$.
(3)直线l的普通方程为y-1=$\frac{\sqrt{3}}{3}$(x-1),即y=$\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}+1$.
联立方程组$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}+1}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,消元得2x2+(1-$\sqrt{3}$)x-4-$\sqrt{3}$=0.
设A(x1,y1),B(x2,y2),
则x1+x2=$\frac{\sqrt{3}-1}{2}$,y1+y2=$\frac{\sqrt{3}}{3}$(x1+x2)-$\frac{2\sqrt{3}}{3}$+2=$\frac{15-5\sqrt{3}}{6}$.
∴AB的中点坐标为($\frac{\sqrt{3}-1}{4}$,$\frac{15-5\sqrt{3}}{12}$).
点评 本题考查了直线的参数方程,参数的几何意义,直线的交点坐标,属于中档题.

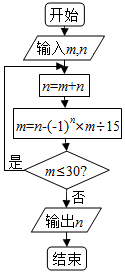 执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )
执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )| A. | 50 | B. | 35 | C. | 20 | D. | 15 |
| A. | 180个 | B. | 196个 | C. | 210个 | D. | 224个 |
| A. | [$\frac{14}{3}$,$\frac{37}{3}$] | B. | [$\frac{1}{3}$,$\frac{50}{3}$] | C. | [$\frac{11}{3}$,6] | D. | [$\frac{41}{6}$,$\frac{22}{3}$] |
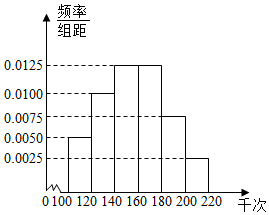 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示