题目内容
若△ABC的三边长a，b，c满足（a+b-c）（a+b+c）=ab，则角C的大小是（ ）
| A．60° | B．90° | C．120° | D．150° |
∵（a+b-c）（a+b+c）=ab
∴（a+b）2-c2=ab 即a2+b2-c2=-ab
根据余弦定理可知cosC=
=
=-
∴∠C=120°
故选C．
∴（a+b）2-c2=ab 即a2+b2-c2=-ab
根据余弦定理可知cosC=
| a2+b2-c2 |
| 2ab |
| -ab |
| 2ab |
| 1 |
| 2 |
∴∠C=120°
故选C．
练习册系列答案
相关题目
若△ABC的三边长a，b，c满足（a+b-c）（a+b+c）=ab，则角C的大小是（ ）
| A、60° | B、90° | C、120° | D、150° |
=（sinx，
cosx），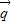
=（cosx，cosx），定义函数f（x）=