题目内容
11．（x+y）（$\frac{1}{x}$+y）5的展开式中，含x-2y2的项的系数为10．分析 把所给的式子用二项式定理展开，可得展开式中x-2y2的系数．
解答 解：（x+y）（$\frac{1}{x}$+y）5 =（x+y）（${C}_{5}^{0}\frac{1}{{x}^{5}}+{C}_{5}^{1}\frac{1}{{x}^{4}}y+{C}_{5}^{2}\frac{1}{{x}^{3}}{y}^{2}+{C}_{5}^{3}\frac{1}{{x}^{2}}{y}^{3}$$+{C}_{5}^{4}\frac{1}{x}{y}^{4}+{C}_{5}^{5}{y}^{5}$），
∴展开式中含x-2y2的项的系数为${C}_{5}^{2}=10$．
故答案为：10．
点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
2．曲线y=$\frac{1}{2}$x2-2x在x=3处的切线的倾斜角为（ ）
| A． | 45° | B． | -45° | C． | 135° | D． | -135° |
16．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x+2y≤8}\\{2x+y≤8}\\{x≥0}\\{y≥0}\end{array}\right.$ 则目标函数z=6x+2y-1的最大值为（ ）
| A． | 17 | B． | 20 | C． | 21 | D． | 23 |
1．已知a，b为异面直线，下列结论不正确的是（ ）
| A． | 必存在平面α使得a∥α，b∥α | |
| B． | 必存在平面α使得a，b与α所成角相等 | |
| C． | 必存在平面α使得a?α，b⊥α | |
| D． | 必存在平面α使得a，b与α的距离相等 |
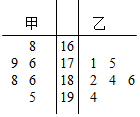在一次水稻试验田验收活动中，将甲、乙两种水稻随机抽取各6株样品，单株籽粒数制成如图所示的茎叶图：