题目内容

3．数列{an}满足：a1=1，an=an-1+3n，则a4等于（　　）
A．4B．13C．28D．43

分析 利用数列的递推关系式，逐步求解即可．

解答 解：数列{an}满足：a1=1，an=an-1+3n，
可得a2=a1+3=1+3×2=7，
a3=a2+3×3=7+9=16，
a4=a3+3×4=28．
故选：C．

点评 本题考查数列的递推关系式的应用，考查计算能力．

练习册系列答案
相关题目
13．若数列{an}的前n项和为Sn=kn2+n，且a10=39，则a100=（　　）
A．200B．199C．299D．399
14．数列{an}的前n项和为Sn，满足2Sn+an=1．设${a_n}=\frac{{{b_n}-n}}{2n+1}$．
（1）求：求数列{an}和{bn}的通项公式；
（2）设{bn}的前n项和为Tn，求$\frac{{{T_n}+18}}{n}+\frac{n+2}{n}{（\frac{1}{3}）^n}$的最小值．
11．已知直线l过点P（3，-2）且与椭圆$C：\frac{x^2}{20}+\frac{y^2}{16}=1$相交于A，B两点，则使得点P为弦AB中点的直线斜率为（　　）
A．$-\frac{3}{5}$B．$-\frac{6}{5}$C．$\frac{6}{5}$D．$\frac{3}{5}$
18．为了了解某校学生喜欢吃辣是否与性别有关，随机对此校100人进行调查，得到如下的列表：已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$．
喜欢吃辣不喜欢吃辣合计
男生401050
女生203050
合计6040100
（1）请将上面的列表补充完整；
（2）是否有99.9%以上的把握认为喜欢吃辣与性别有关？说明理由：
下面的临界值表供参考：
p（K2≥k）0.100.050.0250.0100.0050.001
k2.7063.8415.0246.6357.87910.828
（参考公式：${K^2}=\frac{{n•{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d）
8．不等式logax-ln2x＜4（a＞0，且a≠1）对任意x∈（1，100）恒成立，则实数a的取值范围为（0，1）∪（${e}^{\frac{1}{4}}$，+∞）．
15．函数$y={log_a}{x^2}$的零点为（　　）
A．±1B．（±1，0）C．1D．（1，0）
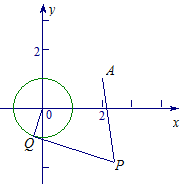12．已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|．
（Ⅰ）求实数a、b间满足的等量关系；
（Ⅱ） 求线段PQ长的最小值；
（Ⅲ） 若以P为圆心所作的圆P与圆O有公共点，试求半径取最小值时圆P的方程．
13．三个数a=0.32，b=0.32.1，c=20.3的大小关系是（　　）
A．a＜b＜cB．a＜c＜bC．b＜a＜cD．b＜c＜a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网