题目内容
数列{an}满足a1+
+
+…+
=3n-2(n∈N*,n≥1),则an= .
| a2 |
| 2 |
| a3 |
| 3 |
| an |
| n |
考点:数列递推式
专题:等差数列与等比数列
分析:由数列{an}满足a1+
+
+…+
=3n-2(n∈N*,n≥1),得a1+
+
+…+
=3n-1-2(n∈N*,n≥2),由此能求出an=
.
| a2 |
| 2 |
| a3 |
| 3 |
| an |
| n |
| a2 |
| 2 |
| a3 |
| 3 |
| an-1 |
| n-1 |
|
解答:
解:∵数列{an}满足a1+
+
+…+
=3n-2(n∈N*,n≥1),①
∴a1+
+
+…+
=3n-1-2(n∈N*,n≥2),②
∴①-②,得
=3n-3n-1=
•3n-1=2•3n-2,n≥2,
∴an=2n•3n-2,
又a1=3-2=1,不满足上式,
∴an=
.
故答案为:
.
| a2 |
| 2 |
| a3 |
| 3 |
| an |
| n |
∴a1+
| a2 |
| 2 |
| a3 |
| 3 |
| an-1 |
| n-1 |
∴①-②,得
| an |
| n |
| 2 |
| 3 |
∴an=2n•3n-2,
又a1=3-2=1,不满足上式,
∴an=
|
故答案为:
|
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3名同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2x-1+log2x的零点所在的一个区间是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(1,2) |
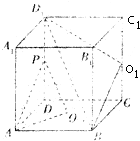 如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证:
如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证: 所有正奇数如图数表排列(图中下一行中的数的个数是上一行中数的个数的2倍),则第m行中的第n个数是
所有正奇数如图数表排列(图中下一行中的数的个数是上一行中数的个数的2倍),则第m行中的第n个数是