题目内容
设F是双曲线C:
-
=1的右焦点,l是双曲线C的一条渐近线,过F作一条直线垂直与l,垂足为P,则sin∠OFP的值为( )
| x2 |
| 16 |
| y2 |
| 9 |
分析:双曲线C:
-
=1的右焦点,F(5,0),双曲线C的一条渐近线l的方程为4x+3y=0.利用点到直线的距离公式,求出|PF|,由此能求出sin∠OFP.
| x2 |
| 16 |
| y2 |
| 9 |
解答: 解:∵F是双曲线C:
解:∵F是双曲线C:
-
=1的右焦点,
∴F(5,0),
∵l是双曲线C的一条渐近线,
∴l的方程可以为4x+3y=0.
利用点到直线的距离公式,知|PF|=
=4,
∵|OF|=5,
∴sin∠OFP=
=
.
故选B.
 解:∵F是双曲线C:
解:∵F是双曲线C:| x2 |
| 16 |
| y2 |
| 9 |
∴F(5,0),
∵l是双曲线C的一条渐近线,
∴l的方程可以为4x+3y=0.
利用点到直线的距离公式,知|PF|=
| |20+0| | ||
|
∵|OF|=5,
∴sin∠OFP=
| |PF| |
| |OF| |
| 4 |
| 5 |
故选B.
点评:本题考查双曲线的简单性质,解题时要认真审题,恰当运用数形结合思想,注意合理地进行等价转化.

练习册系列答案
相关题目
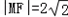 ,求点M的坐标;
,求点M的坐标; )的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。
)的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。 ,求直线l的方程.
,求直线l的方程.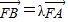 ,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.
,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.