题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的左、右焦点为F1 ， F2 ， 设点F1 ， F2与椭圆短轴的一个端点构成斜边长为4的直角三角形．
（1）求椭圆C的标准方程；
（2）设A，B，P为椭圆C上三点，满足 
= 
+ 
，记线段AB中点Q的轨迹为E，若直线l：y=x+1与轨迹E交于M，N两点，求|MN|．
【答案】
（1）
解：∵点F1，F2与椭圆短轴的一个端点构成斜边长为4的直角三角形．
∴2c=4，b=2，
故c=2，a=2 
，
故椭圆C的标准方程为： 
（2）
解：设A（2 cosα，2sinα），B（2 cosβ，2sinβ），
∵ 
= 
+ 
，
∴ =（ 
， 
），
∵点P在椭圆上，
∴（3cosα+4cosβ）2+（3sinα+4sinβ）2=25，
∴cosαcosβ+sinαsinβ=0，
∴cos（α﹣β）=0，
∴a﹣β= 
，
∴B（2 sinα，﹣2cosα），
∴AB中点Q的坐标为（ cosα+ sinα，sinα﹣cosα），
设Q的点坐标为（x，y），
∴x= cosα+ sinα，y=sinα﹣cosα，
∴ 
=cos2α+2cosαsinα+sin2α=1+2cosαsinα，y2=cos2α﹣2cosαsinα+sin2α=1﹣2cosαsinα
∴ +y2=2，
即线段AB中点Q的轨迹为E的方程为 
，
设M，N两点的坐标为（x1，y1），（x2，y2），
由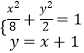 
，消y，整理得5x2+8x﹣4=0，
∴x1+x2=﹣ 
，x1x2=﹣ ，
∴|MN|= 
|x1﹣x2|= 
= 
= 
．
【解析】（1）由题意可得c=2，即可求出b=2，即可求出椭圆的标准方程，（2）设A（2 cosα，2sinα），B（2 cosβ，2sinβ），根据题意和点P在椭圆上，化简整理可得a﹣β= ，再根据中点坐标公式，消α，线段AB中点Q的轨迹为E的方程为 ，再设M，N两点的坐标为（x1 ， y1），（x2 ， y2），根据弦长公式即可求出．
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：
，焦点在y轴：
．
