题目内容
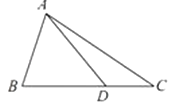
【题目】在△ABC中,D在AB上,AD:DB=1:2,E为AC中点,CD、BE相交于点P,连结AP.设 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),则x,y的值分别为( )
(x,y∈R),则x,y的值分别为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:由D、P、C三点共线,则存在实数λ使得 ![]() =λ
=λ ![]() =λ(
=λ( ![]() ﹣
﹣ ![]() ), ∴
), ∴ ![]() ﹣
﹣ ![]() =
= ![]() =λ(
=λ( ![]() ﹣
﹣ ![]() ),
),
∴ ![]() =λ
=λ ![]() +(1﹣λ)
+(1﹣λ) ![]() ,
,
∵AD:DB=1:2,
∵ ![]() =
= ![]()
![]() ,
,
∴ ![]() =λ
=λ ![]() +
+ ![]() (1﹣λ)
(1﹣λ) ![]() ,
,
由E为AC中点,由E、P、B三点共线,同理存在实数μ使得 ![]() =
= ![]()
![]() +μ
+μ ![]() ,
,
∴ 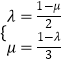 ,
,
解得 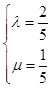
∴ ![]() =
= ![]()
![]() +
+ ![]()
![]() ,
,
∵ ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),
(x,y∈R),
∴x= ![]() ,y=
,y= ![]() ,
,
故选:C
【考点精析】关于本题考查的平面向量的基本定理及其意义,需要了解如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目