题目内容
已知函数h(x)=ax,(a>1),g(x)=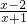 ,f(x)=h(x)+g(x)
,f(x)=h(x)+g(x)
①写出f(x)的解析式及定义域;
②求证函数f(x)在(-1,+∞)上为增函数;
③求证方程f(x)=0没有负数根.
解:①∵h(x)=ax,(a>1),g(x)=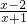 ,f(x)=h(x)+g(x)
,f(x)=h(x)+g(x)
∴ (a>1),
(a>1),
定义域(-∞,-1)∪(-1,+∞)…
证明:②设-1<x1<x2,
则 =
= ,
,
∵-1<x1<x2,∴x1+1>0,x2+1>0,x1-x2<0,
∴ ;
;
∵-1<x1<x2,且a>1,∴ ,∴
,∴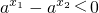 ,
,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(-1,+∞)上为增函数;…
③假设x0是方程f(x)=0的负数根,且x0≠-1,则 ,
,
即 ,①
,①
当-1<x0<0时,0<x0+1<1,∴ ,∴
,∴ ,
,
而由a>1知 ,∴①式不成立;
,∴①式不成立;
当x0<-1时,x0+1<0,∴ ,∴
,∴ ,
,
而 ,∴①式不成立.
,∴①式不成立.
综上所述,方程f(x)=0没有负数根.…
分析:①根据已知中f(x)=h(x)+g(x),可得函数的解析式,进而根据使函数解析式有意义的原则,可求出函数的定义域;
②-1<x1<x2,做差判断f(x1)与f(x2)的大小,进而根据函数单调性的定义,可判断出函数f(x)在(-1,+∞)上为增函数;
③假设x0是方程f(x)=0的负数根,且x0≠-1,则 ,分当-1<x0<0时和当x0<-1时,讨论其存在性,最后综合讨论结果,可得答案.
,分当-1<x0<0时和当x0<-1时,讨论其存在性,最后综合讨论结果,可得答案.
点评:本题考查的知识点是函数的解析式,函数的定义域,函数的单调性,函数的零点,是函数较为综合的应用,难度比较大,属于难题.
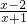 ,f(x)=h(x)+g(x)
,f(x)=h(x)+g(x)∴
 (a>1),
(a>1),定义域(-∞,-1)∪(-1,+∞)…
证明:②设-1<x1<x2,
则
 =
= ,
,∵-1<x1<x2,∴x1+1>0,x2+1>0,x1-x2<0,
∴
 ;
;∵-1<x1<x2,且a>1,∴
 ,∴
,∴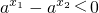 ,
,∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(-1,+∞)上为增函数;…
③假设x0是方程f(x)=0的负数根,且x0≠-1,则
 ,
,即
 ,①
,①当-1<x0<0时,0<x0+1<1,∴
 ,∴
,∴ ,
,而由a>1知
 ,∴①式不成立;
,∴①式不成立;当x0<-1时,x0+1<0,∴
 ,∴
,∴ ,
,而
 ,∴①式不成立.
,∴①式不成立.综上所述,方程f(x)=0没有负数根.…
分析:①根据已知中f(x)=h(x)+g(x),可得函数的解析式,进而根据使函数解析式有意义的原则,可求出函数的定义域;
②-1<x1<x2,做差判断f(x1)与f(x2)的大小,进而根据函数单调性的定义,可判断出函数f(x)在(-1,+∞)上为增函数;
③假设x0是方程f(x)=0的负数根,且x0≠-1,则
 ,分当-1<x0<0时和当x0<-1时,讨论其存在性,最后综合讨论结果,可得答案.
,分当-1<x0<0时和当x0<-1时,讨论其存在性,最后综合讨论结果,可得答案.点评:本题考查的知识点是函数的解析式,函数的定义域,函数的单调性,函数的零点,是函数较为综合的应用,难度比较大,属于难题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
