题目内容
记函数f(x)=
(a≠0且a≠-1).
(1)试求函数f(x)的定义域和值域;
(2)已知函数h(x)=f(2x),且函数y=h(x)为奇函数,求实数a的值;
(3)记函数g(x)=h(x-1)+1,试计算g(-1)+g(0)+g(1)+g(2)+g(3)的值.
| x-1 | ax+1 |
(1)试求函数f(x)的定义域和值域;
(2)已知函数h(x)=f(2x),且函数y=h(x)为奇函数,求实数a的值;
(3)记函数g(x)=h(x-1)+1,试计算g(-1)+g(0)+g(1)+g(2)+g(3)的值.
分析:(1)将f(x)=
分离出常数,得到f(x)=
-
,即可求得函数f(x)的定义域和值域;
(2)由h(x)=f(2x)=
,利用h(-x)=-h(x)即可求得a的值;
(3)由题意可得y=g(x)的图象关于点(1,1)对称,于是对任意的x1,x2∈R,都有当x1+x2=2时,g(x1)+g(x2)=2,从而可得答案.
| x-1 |
| ax+1 |
| 1 |
| a |
| ||
| ax+1 |
(2)由h(x)=f(2x)=
| 2x-1 |
| a•2x+1 |
(3)由题意可得y=g(x)的图象关于点(1,1)对称,于是对任意的x1,x2∈R,都有当x1+x2=2时,g(x1)+g(x2)=2,从而可得答案.
解答:.解:(1)∵f(x)=
=
=
-
,
∴函数f(x)的定义域为{x|x≠-
,x∈R};值域为{y|y≠
,y∈R},
(2)h(x)=f(2x)=
,
因为,y=h(x)为奇函数,所以h(-x)=-h(x),
即
=-
=
,
整理得22x-a=a•22x-1对任意x成立,所以a=1.
(3)因为g(x)=h(x-1)+1,所以y=g(x)的图象是由奇函数y=h(x)的图象向右平移一个单位,再向上平移一个单位得到的,
即y=g(x)的图象关于点(1,1)对称,从而对任意的x1,x2∈R,都有当x1+x2=2时,g(x1)+g(x2)=2,
∴g(-1)+g(3)=g(0)+g(2)=2,又g(1)=1,
∴g(-1)+g(0)+g(1)+g(2)+g(3)=5.
| x-1 |
| ax+1 |
| ||||
| ax+1 |
| 1 |
| a |
| ||
| ax+1 |
∴函数f(x)的定义域为{x|x≠-
| 1 |
| a |
| 1 |
| a |
(2)h(x)=f(2x)=
| 2x-1 |
| a•2x+1 |
因为,y=h(x)为奇函数,所以h(-x)=-h(x),
即
| 2x-1 |
| a•2x+1 |
| 2-x-1 |
| a•2-x+1 |
| 2x-1 |
| a+2x |
整理得22x-a=a•22x-1对任意x成立,所以a=1.
(3)因为g(x)=h(x-1)+1,所以y=g(x)的图象是由奇函数y=h(x)的图象向右平移一个单位,再向上平移一个单位得到的,
即y=g(x)的图象关于点(1,1)对称,从而对任意的x1,x2∈R,都有当x1+x2=2时,g(x1)+g(x2)=2,
∴g(-1)+g(3)=g(0)+g(2)=2,又g(1)=1,
∴g(-1)+g(0)+g(1)+g(2)+g(3)=5.
点评:本题考查函数奇偶性的性质,考查函数的图象与图象变化,突出转化思想的考查运用,考查中心对称问题,综合性强,运算量大,是难题.

练习册系列答案
相关题目
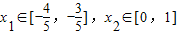 ,试求a的取值范围;
,试求a的取值范围;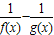 对任意x1,x2∈[1,3]恒有|H(x1)-H(x2)|≤a成立,试求a的取值范围.(参考:ln2≈0.7)
对任意x1,x2∈[1,3]恒有|H(x1)-H(x2)|≤a成立,试求a的取值范围.(参考:ln2≈0.7)