题目内容
已知两点A（3，-4），B（-9，2），在直线AB上求一点P，使|
|=
|
|.
思路分析：由||=||是线段长度之间的比例关系，又由于P在AB上所以可得
=
或
=-
.
解：∵P在AB上且|
|=
|
|可得
=
或
=-
.设P（x,y），
若
=
，
则（x-3,y+4）=
(-9-3,2+4)=(-4,2)，
∴
∴P（-1，-2）.
若
=-
，
则（x-3,y+4）
=-
(-9-3,2+4)=(4,-2),
∴
∴P(7,-6).
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知两点A（-3，4），B（3，2），过点P（2，-1）的直线l与线段AB有公共点，则直线l的倾斜角α的取值范围是（ ）
| A、[0，arctan3] | ||
B、[arctan3，
| ||
C、[
| ||
D、[0，arctan3]∪[
|
与线段AB有公共点，求直线
]
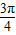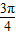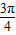，π）
，π）