题目内容
已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,fn(x)=fn-1′(x),则f2 007(x)等于A.sinx B.-sinx
C.cosx D.-cosx
解析:由已知,有f1(x)=cosx,f2(x)=-sinx,f3(x)=-cosx,f4(x)=sinx,f5(x)=cosx,…,可以归纳出:
f4n(x)=sinx,f4n+1(x)=cosx,f4n+2(x)=-sinx,f4n+3(x)=-cosx(n∈N*).
∴f2 007(x)=f3(x)=-cosx.
答案:D
练习册系列答案
相关题目
已知f1(x)=cosx,f2(x)=cosωx(ω＞0),f2(x)的图象可以看作是把f1(x)的图象在其所在的坐标系中的横坐标压缩到原来的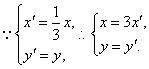
倍（纵坐标不变）而得到的，则ω为( )
倍（纵坐标不变）而得到的，则ω为( )A.
B.2
C.3
D.
倍（纵坐标不变）而得到的，则ω为( )
B.2 C.3 D.
倍（纵坐标不变）而得到的，则ω为( )
