题目内容
在△ABC,角A、B、C所对的边分别为a,b,c,满足
=
(Ⅰ)求角C;
(Ⅱ)若c=
,且△ABC的面积为
,求a+b的值.
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
(Ⅰ)求角C;
(Ⅱ)若c=
| 7 |
3
| ||
| 2 |
考点:余弦定理的应用,正弦定理的应用
专题:计算题,三角函数的求值,解三角形
分析:(Ⅰ)运用正弦定理,将角化为边,再由余弦定理,即可得到角C;
(Ⅱ)运用三角形的面积公式,可得ab=6,再由余弦定理,配方可得a+b.
(Ⅱ)运用三角形的面积公式,可得ab=6,再由余弦定理,配方可得a+b.
解答:
解:(Ⅰ)由正弦定理
=
即为
=
,即b(a-b)=(a+c)(a-c),
即有a2+b2-c2=ab,
由余弦定理可得cosC=
=
=
,
由于C为三角形的内角,则C=
;
(Ⅱ)c2=a2+b2-2abcos60°=a2+b2-ab,
即有a2+b2-ab=7,
即(a+b)2-3ab=7,
S△ABC=
absin60°=
,
即ab=6,
则(a+b)2=7+3ab=7+18=25,
则有a+b=5.
| a+c |
| b |
| sinA-sinB |
| sinA-sinC |
| a+c |
| b |
| a-b |
| a-c |
即有a2+b2-c2=ab,
由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| ab |
| 2ab |
| 1 |
| 2 |
由于C为三角形的内角,则C=
| π |
| 3 |
(Ⅱ)c2=a2+b2-2abcos60°=a2+b2-ab,
即有a2+b2-ab=7,
即(a+b)2-3ab=7,
S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
即ab=6,
则(a+b)2=7+3ab=7+18=25,
则有a+b=5.
点评:本题考查正弦定理和余弦定理及面积公式的运用,考查运算能力,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知向量
=(2m,1),向量
=(1,-8),若
⊥
,则实数m的值是( )
| a |
| b |
| a |
| b |
| A、-4 | ||
| B、4 | ||
C、
| ||
D、
|
现有男生4人女生5人,从中选2名男生1名女生参加数学、物理、化学三科竞赛,要求每科均有1人参加,每名学生只参加一科竞赛,则不同的参赛方法有( )
| A、15种 | B、30种 |
| C、90种 | D、180种 |
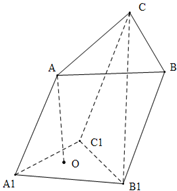 在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为
在三棱柱ABC-A1B1C1中,底面△ABC为正三角形且边长为