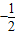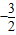题目内容
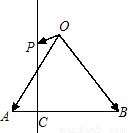
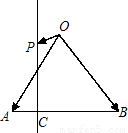
 如图,在等腰直角△ABC中,∠C=90°,|AB|=2
如图,在等腰直角△ABC中,∠C=90°,|AB|=2| 2 |
求(1)
| AC |
| AB |
(2)
| CA |
| AB |
(3)
| BC |
| CA |
| AB |
分析:在等腰直角△ABC中,∠C=90°,|AB|=2
,容易求|
|、|
|的模,向量
与
的夹角45°,
根据公式可以求得(1)、(2)的数量积的值;展开(3)分别求数量积的值,再求其和.
| 2 |
| AC |
| AB |
| AC |
| AB |
根据公式可以求得(1)、(2)的数量积的值;展开(3)分别求数量积的值,再求其和.
解答:解:在等腰直角△ABC中,∠A=45°,∠C=45°,|AC|=|BC|=2
(1)
•
=|
||
|cos45°=2
.
(2)
•
=|
|•|
|cos135°=-4.
(3)
•(
+
)=
•
+
•
=|
|•|
|cos90°+|
|•|
|cos135°=-4
(1)
| AC |
| AB |
| AC |
| AB |
| 2 |
(2)
| CA |
| AB |
| CA |
| AB |
(3)
| BC |
| CA |
| AB |
| BC |
| CA |
| BC |
| AB |
| BC |
| CA |
| BC |
| AB |
点评:本题考查平面向量数量积的运算,数形结合的数学思想,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
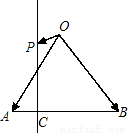
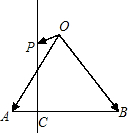 如图,在等腰直角△ABO中,设
如图,在等腰直角△ABO中,设 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( ) 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,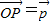 ,则
,则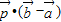 =( )
=( )
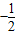



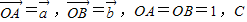 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,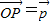 ,则
,则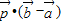 =( )
=( )
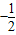

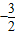

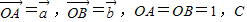 为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,
为AB上靠近点A的四等分点,过C作AB的垂线L,设P为垂线上任一点,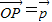 ,则
,则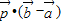 =( )
=( )