Question

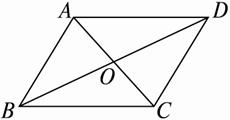
如图2-2-7所示,在半径为1的⊙O中，引两条互相垂直的直径AE和BF，在上取点C，弦AC交BF于P，弦CB交AE于Q.证明四边形APQB的面积是1.

图2-2-7

Answer 1

思路分析：由已知条件可以证明四边形ABEF是正方形，且边长为2，则正方形面积为2.

而△ABD的面积为正方形面积的一半，所以，只需证明S_{四边形APQB}=S_△ABD，即证S_△BPD=S_△BPQ，即证DQ∥PB.

因为BP⊥AE，所以，只需证DQ⊥AE.

证明：∵AE、BF为互相垂直的两条直径，垂足O为圆心，

∴AE、BF互相平分、垂直且相等.

∴四边形ABEF是正方形.

∴∠ACB=∠AEF=45°，

即∠DCQ=∠QED.

∴D、Q、E、C四点共圆.连结CE、DQ，则∠DCE+∠DQE=180°.

∵AE为⊙O的直径，

∴∠DCE=90°，∠DQE=90°.

∵∠FOE=90°，进而DQ∥BF，

∴S_△BPQ=S_△BPD.

∴S_△ABP+S_△BPQ=S_△ABP+S_△BPD，即S_{四边形ABQP}=S_△ABD.

∵⊙O的半径为1，∴正方形边长为，即AB=AF=.

∴S_{四边形ABQP}=S_△ABD=AB·AF=1.

    方法归纳 当题目的结论直接证明较繁或无法证明时，可根据条件先证明某四点共圆，再利用圆的性质可使问题得以解决，这种方法常称之为“作辅助圆”方法.