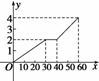
题目内容
已知函数f(x)对一切x，y∈R，都有f(x＋y)＝f(x)＋f(y)．
(1)求证：f(x)是奇函数；
(2)若f(－3)＝a，用a表示f(12)．
(1)证明 显然f(x)的定义域是R，它关于原点对称．
在f(x＋y)＝f(x)＋f(y)中，令y＝－x，
得f(0)＝f(x)＋f(－x)，令x＝y＝0，
得f(0)＝f(0)＋f(0)，∴f(0)＝0，
∴f(
x)＋f(－x)＝0，即f(－x)＝－f(x)，
∴f(x)是奇函数．
(2)解 由f(－3)＝a，f(x＋y)＝f(x)＋f(y)及f(x)是奇函数，得f(12)＝2f(6)＝4f(3)＝－4f(－3)＝－4a.
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
，其生产的总成本y(万元)与年
－48x＋8 000，已知此生产线年产量最大为210吨．
＝4，则f(2 011)的值为_____．
恒成立，求实数m的取值
(x≠±1)，则f(－3
4＋3x－x2)的单调递减区间是________________．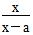
(x≠a)．