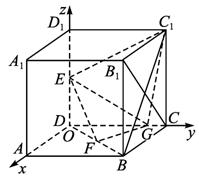
题目内容
已知在正方体ABCD—A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=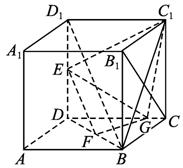
(1)求证:EF⊥B1C;
(2)求EF与C1G所成角的余弦值;
(3)求二面角F—EG—C1的大小(用反三角函数表示).
解法一:(1)连结D1B、BC1,

∵E、F是D1D、BD的中点,
∴EF∥D1B,且EF=![]() D1B.
D1B.
又∵D1C1⊥平面BC1,∴D1B在平面BC1上的射影为BC1.
∵BC1⊥B1C,由三垂线定理知B1C⊥D1B.
∴EF⊥B1C.
(2)延长CD至点P,使DP=CG,连结D1P、PB,
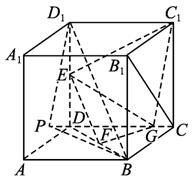
∴D1C1![]() PG.
PG.
∴四边形D1C1GP为平行四边形.
∴D1P![]() C1G.
C1G.
又由(1)知,EF∥D1B,
∴∠PD1B为异面直线EF与C1G所成的角.
设正方体的棱长为4,则D1P2=42+12=17,D1B2=42+42+42=48,PB2=42+52=41.
∴cos∠PD1B=![]() .
.
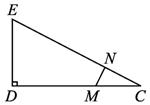
(3)取DC的中点M,连结FM,则FM⊥DC,
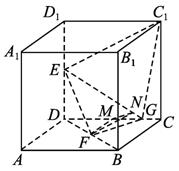
过M作MN⊥EG于N点,连结FN.
由三垂线定理可证FN⊥EG.∴∠MNF的邻补角为二面角F—EG—C1的平面角.
设正方体的棱长为4,则FM=2,
在Rt△EDG中,△EDG∽△MNG,∴MN=![]() .
.
在Rt△FMN中,∠FMN=90°,∴tan∠MNF=![]() .
.
∴∠MNF=arctan![]() .
.
∴二面角F—EG—C1的大小为π-arctan![]() .
.
解法二:建立下图所示空间直角坐标系O—xyz,设正方体的棱长为4,则E(0,0,2),F(2,2,0),C(0,4,0),B(4,4,0),C1(0,4,4),B1(4,4,4),G(0,3,0).
(1) ![]() =(2,2-2),
=(2,2-2),![]() =(-4,0,-4),
=(-4,0,-4),
∴![]() ·
·![]() =2×(-4)+2×0+(-2)×(-4)=0.
=2×(-4)+2×0+(-2)×(-4)=0.
∴![]() ⊥
⊥![]() .∴EF⊥B1C.
.∴EF⊥B1C.
(2) ![]() =(0,-1,-4),
=(0,-1,-4),
∴![]() ·
·![]() =2×0+2×(-1)+(-2)×(-4)=6.
=2×0+2×(-1)+(-2)×(-4)=6.
又∵|![]() |=
|=![]() ,|
,|![]() |=2
|=2![]() ,
,
∴cos〈![]() ,
,![]() 〉=
〉= =
=![]() .
.
(3)(*有个别学生按超出课本要求的方法求解,按此标准给分)
平面D1DCC1的法向量为![]() =(-4,0,0),设平面EFG的法向量为n=(x,y,z),
=(-4,0,0),设平面EFG的法向量为n=(x,y,z),
∴ 即
即![]()
令x=1,则y=2,z=3.∴n=(1,2,3).
∴cos〈n,![]() 〉=
〉=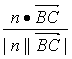 =
=![]() .
.
∴二面角F—EG—C1的大小为π-arccos![]() .
.

 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG= 已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=
已知在正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=

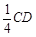 .
. 