题目内容
(12分) 已知在正方体ABCD —A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG =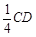 .
.

(1)求证:EF⊥B1C;
(2)求EF与G C1所成角的余弦值;
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(12分) 已知在正方体ABCD —A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG =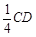 .
.

(1)求证:EF⊥B1C;
(2)求EF与G C1所成角的余弦值;
 阅读快车系列答案
阅读快车系列答案