题目内容
如图,已知在正方体ABCD—A′B′C′D′中,面对角线AB′、BC′上分别有两点E、F,且B′E=C′F,
求证:(1)EF∥平面ABCD;
(2)平面ACD′∥平面A′BC′.
思路解析:对于第(1)问,证明直线与平面平行可以从线线平行入手,也可以从面面平行入手来证.而对于第(2)问,一般可以转化为线线平行.
(1)证法一:(由线线平行证线面平行)
过点E、F分别作AB、BC的垂线EM、FN分别交AB、BC于点M、N,连结MN.
∵BB′⊥平面ABCD,∴BB′⊥AB,BB′⊥BC.
∴EM∥BB′,FN∥BB′.∴EM∥FN.
∵AB′=BC′,B′E=C′F,∴AE=BF.
又∠B′AB=∠C′BC=45°,∴Rt△AME≌Rt△BNF.
∴EM=FN,四边形MNFE是平行四边形.
∴EF∥MN.又MN![]() 平面ABCD,∴EF∥平面ABCD.
平面ABCD,∴EF∥平面ABCD.
证法二:(由面面平行证线面平行)
过点E作EG∥AB交BB′于点G,连结GF.∴![]()
∵B′E=C′F,B′A=C′B,∴![]() .∴FG∥B′C∥BC.
.∴FG∥B′C∥BC.
又∵EG∩FG=G,AB∩BC=B,∴平面EFG∥平面ABCD.
又EF![]() 平面EFG,∴EF∥平面ABCD.
平面EFG,∴EF∥平面ABCD.
(2)证明:(由线线平行证面面平行)

如图9-3-18,∵在正方体ABCD—A′B′C′D′中,AD′∥BC′,CD′∥BA′,
又AD′∩CD′=D′,BC′∩BA′=B,∴平面ACD′∥平面A′BC′.
方法归纳 一般来说,线线关系、面面关系都转化为由线面关系来分析解决.该题证明线面平行用了两种证法.证法一利用了线面平行的判定定理,即由线线平行来证明线面平行;证法二利用了面面平行的性质定理,即由面面平行证明线面平行.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知魔方ABCD-EFGH,一只在点A处蚂蚁先从前面ABFE,再从右面BCGF爬到点G的最短爬法(蚂蚁只能沿每个小正方体的棱爬行)共有( )种.
如图,已知魔方ABCD-EFGH,一只在点A处蚂蚁先从前面ABFE,再从右面BCGF爬到点G的最短爬法(蚂蚁只能沿每个小正方体的棱爬行)共有( )种.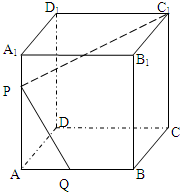 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.