题目内容
设函数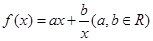 ,若
,若 在点
在点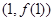 处的切线斜率为
处的切线斜率为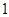 .
.
(Ⅰ)用 表示
表示 ;
;
(Ⅱ)设 ,若
,若 对定义域内的
对定义域内的 恒成立,
恒成立,
(ⅰ)求实数 的取值范围;
的取值范围;
(ⅱ)对任意的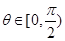 ,证明:
,证明: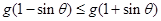 .
.
(Ⅰ)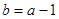 (Ⅱ)详见解析.
(Ⅱ)详见解析.
解析试题分析:(Ⅰ) 利用导数的几何意义“曲线在某点处的导数值等于该点处切线的斜率”来求;(Ⅱ)利用导数研究单调性,进而求最值.
试题解析:(Ⅰ)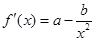 ,依题意有:
,依题意有: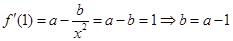 ;
;
(Ⅱ)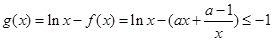 恒成立.
恒成立.
(ⅰ) 恒成立,即
恒成立,即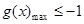 .
.
方法一: 恒成立,则
恒成立,则 .
.
当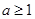 时,
时, ,
,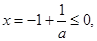

则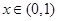 ,
, ,
, 单调递增,
单调递增,
当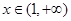 ,
,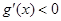 ,
, 单调递减,
单调递减,
则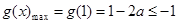 ,符合题意,即
,符合题意,即 恒成立.
恒成立.
所以,实数 的取值范围为
的取值范围为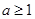 .
.
方法二: ,
,
①当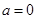 时,
时,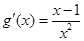 ,
,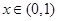 ,
,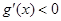 ,
, 单调递减,当
单调递减,当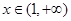 ,
, ,
, 单调递增,则
单调递增,则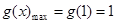 ,不符题意;
,不符题意;
②当 时,
时,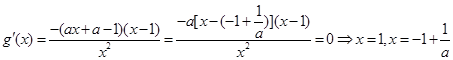 ,
,
(1)若 ,
,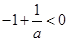 ,
,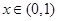 ,
,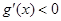 ,
, 单调递减;当
单调递减;当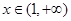 ,
, ,
, 单调递增,则
单调递增,则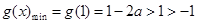 ,不符题意;
,不符题意;
(2)若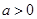 ,
,
若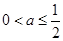 ,
,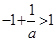 ,
,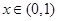 ,
,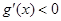 ,
, 单调递减,
单调递减,
这时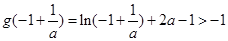 ,不符题意;
,不符题意;
若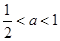 ,
,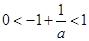 ,
, ,
,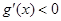 ,
, 单调递减,这时
单调递减,这时 ,不符题意;
,不符题意;
若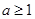 ,
, ,
,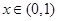 ,
, ,
, 单调递增;当
单调递增;当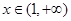 ,
,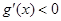 ,
, 单调递减,则
单调递减,则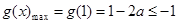 ,符合题意;
,符合题意;
综上,得 恒成立,实数
恒成立,实数 的取值范围为
的取值范围为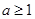 .
.
方法三:易证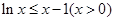

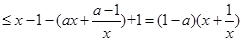
∵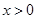 ,∴
,∴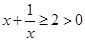 ,
,
当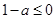 ,即
,即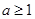 时,
时, ,即
,即 恒成立;
恒成立;
当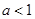

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目

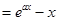 ,其中
,其中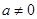 .
.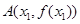 ,
,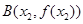
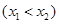 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使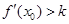 成立?若存在,求
成立?若存在,求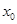 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.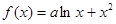 (
( 为实常数)
为实常数) 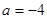 时,求函数
时,求函数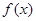 在
在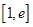 上的最大值及相应的
上的最大值及相应的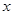 值;
值;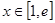 时,讨论方程
时,讨论方程 根的个数
根的个数 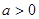 ,且对任意的
,且对任意的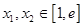 ,都有
,都有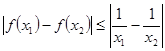 ,求实数a的取值范围
,求实数a的取值范围  .
. 时,求
时,求 在
在 最小值;
最小值; 的取值范围;
的取值范围; (
( ).
). ,设曲线
,设曲线 在与
在与 轴交点处的切线为
轴交点处的切线为 ,
, 为
为 的导函数,满足
的导函数,满足 .
. ,
, ,求函数
,求函数 在
在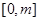 上的最大值;
上的最大值; ,若对于一切
,若对于一切 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.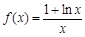 .
. 上存在极值,求实数
上存在极值,求实数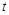 的取值范围;
的取值范围;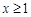 时,不等式
时,不等式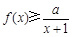 恒成立,求实数
恒成立,求实数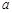 的取值范围.
的取值范围. ,其中
,其中 .
. 时,记
时,记 存在
存在 使
使 成立,求实数
成立,求实数 的取值范围;
的取值范围; 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求 的取值范围.
的取值范围. 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于 的角为
的角为 .
.
 关于
关于