题目内容
(本小题满分16分)如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 与
与 接通.已知
接通.已知 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 与
与 所成的小于
所成的小于 的角为
的角为 .
.
(Ⅰ)求矩形区域 内的排管费用
内的排管费用 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)求排管的最小费用及相应的角 .
.
(Ⅰ) ;(Ⅱ)最小费用为
;(Ⅱ)最小费用为 万元,相应的角
万元,相应的角 为
为 .
.
解析试题分析:(Ⅰ)把 ,
, ,
, 的长度分别用
的长度分别用 表示,分别求出费用相加即可;(Ⅱ)对(Ⅰ)中函数,用导数为工具,判断其单调区间,求出最小值.
表示,分别求出费用相加即可;(Ⅱ)对(Ⅰ)中函数,用导数为工具,判断其单调区间,求出最小值.
试题解析:(Ⅰ)如图,过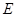 作
作 ,垂足为
,垂足为 ,由题意得
,由题意得 ,
,
故有 ,
, ,
, . 4分
. 4分
所以 5分
5分
 . 8分
. 8分
(Ⅱ)设 (其中
(其中 ),
),
则 . 10分
. 10分
令 得
得 ,即
,即 ,得
,得 . 11分
. 11分
列表
所以当




+ 0 - 
单调递增 极大值 单调递减  时有
时有 ,此时有
,此时有 . 15分
. 15分
答:排管的最小费用为 万元,相应的角
万元,相应的角 . 16分
. 16分
考点:函数的应用、导数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
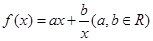 ,若
,若 在点
在点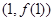 处的切线斜率为
处的切线斜率为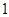 .
. 表示
表示 ;
; ,若
,若 对定义域内的
对定义域内的 恒成立,
恒成立,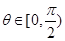 ,证明:
,证明: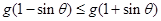 .
. 是定义在
是定义在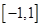 上的奇函数,在
上的奇函数,在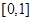 上
上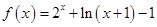 .
. .
.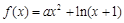 .
.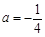 时,求函数
时,求函数 的单调区间;
的单调区间;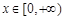 时,不等式
时,不等式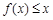 恒成立,求实数
恒成立,求实数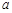 的取值范围.
的取值范围. (
(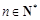 ,e是自然对数的底数).
,e是自然对数的底数). =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线 .
. ,
, ,
, ,
, 的值;
的值; ≥-2时,
≥-2时, ≤
≤ ,求
,求 的取值范围.
的取值范围. -
-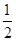 alnx,a∈R.
alnx,a∈R. )≤
)≤ ≤φ′(
≤φ′( ).
). (
(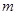 ,
,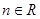 ,
,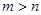 且
且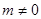 )的图象在
)的图象在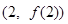 处的切线与
处的切线与 轴平行.
轴平行. 的正、负号;
的正、负号;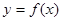 在区间
在区间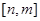 上有最大值为
上有最大值为 ,求
,求 在
在 处取得极值。
处取得极值。 ;
; ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 .
. 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 的值.
的值. 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数