题目内容
(1)在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n取何值时,Sn有最大值,并求出它的最大值.
(2)已知数列{an}的通项公式是an=4n-25,求数列{|an|}的前n项和.
解:(1)由a1=20,S10=S15,解得公差d=- .
.
∵S10=S15,∴S15-S10=a11+a12+a13+a14+a15=0.
∵a11+a15=a12+a14=2a13,∴a13=0,
又∵a1>0,
∴a1、a2、…、a11、a12均为正数,而a14及以后各项均为负数.
∴当n=12或13时,Sn有最大值,为S12=S13=130.
(2)∵an=4n-25,an+1=4(n+1)-25,
∴an+1-an=4=d,又a1=4×1-25=-21.
所以数列{an}是以-21为首项,以4为公差的递增的等差数列,
令
由①得n<6 ;由②得n≥5
;由②得n≥5 ,所以n=6.
,所以n=6.
即数列{|an|}的前6项是以21为首项,公差为-4的等差数列,从第7项起以后各项构成公差为4的等差数列,
而|a7|=a7=4×7-24=3.
设{|an|}的前n项和为Tn,则


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 D.
D.
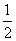 ,an,Sn成等差数列.
,an,Sn成等差数列.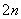 =
=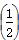 bn,设Cn=
bn,设Cn=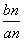 ,求数列{Cn}的前n项和Tn.
,求数列{Cn}的前n项和Tn. ,这样的点P的个数是( )
,这样的点P的个数是( )