题目内容
16.设数列{an}的前n项和为${S_n}={n^2}$,数列{bn}为等比数列,且${a_1}=2{b_1},{\;}^{\;}{b_1}{b_2}=\frac{1}{8}$.(1)求数列{an}和{bn}的通项公式;
(2)设${c_n}=\frac{a_n}{b_n}$,求数列{cn}的前n项和Tn.
分析 (1)由${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,能求出an=2n-1,从而${b}_{1}=\frac{1}{2}$,${b}_{2}=\frac{1}{4}$,由此能求出${b}_{n}=\frac{1}{{2}^{n}}$.
(2)由${c_n}=\frac{a_n}{b_n}$=$\frac{2n-1}{\frac{1}{{2}^{n}}}$=(2n-1)•2n,利用错位相减法能求出数列{cn}的前n项和.
解答 解:(1)∵数列{an}的前n项和为${S_n}={n^2}$,
∴当n≥2时,an=Sn-Sn-1=2n-1,
当n=1时,a1=S1=1,
综上an=2n-1,
∵数列{bn}为等比数列,且${a_1}=2{b_1},{\;}^{\;}{b_1}{b_2}=\frac{1}{8}$,
∴${b}_{1}=\frac{1}{2}$,${b}_{2}=\frac{1}{4}$,∴q=$\frac{1}{2}$,
∴${b}_{n}=\frac{1}{{2}^{n}}$.
(2)${c_n}=\frac{a_n}{b_n}$=$\frac{2n-1}{\frac{1}{{2}^{n}}}$=(2n-1)•2n,
∴数列{cn}的前n项和:
Tn=1×2+3×22+…+(2n-1)•2n,
2Tn=1×22+3×23+…+(2n-1)×2n+1,
两式相减得:
-Tn=2+23+24+…+2n+1-(2n-1)×2n+1
=2+$\frac{8(1-{2}^{n-2})}{1-2}$-(2n-1)×2n+1
=-6-(2n-3)×2n+1,
∴Tn=(2n-3)×2n+1+6.
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | $\frac{1}{19}$ | B. | $\frac{17}{18}$ | C. | $\frac{4}{19}$ | D. | $\frac{2}{17}$ |
| A. | $\sqrt{37}$ | B. | $\sqrt{47}$ | C. | $\sqrt{57}$ | D. | $\sqrt{45}$ |
| A. | $C_{2007}^4$ | B. | $C_{2007}^3$ | C. | $C_{2008}^4$ | D. | $C_{2008}^3$ |
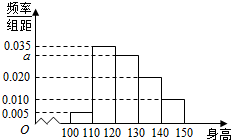 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )