题目内容
若a、b、c都是正数,且至少有一个不为1,axbycz=aybzcx=azbxcy=1,则x、y、z应满足的关系是________.
答案:x+y+z=0或x=y=z
解析:
解析:
解:由axbycz=1,两边取对数,得xlg a+ylg b+zlg c=0,
同理ylg a+zlg b+xlg c=0,zlg a+xlg b+ylg c=0.
三式相加,得(x+y+z)lg a+(x+y+z)lg b+(x+y+z)lg c=0.
∴(x+y+z)(1g a+lg b+lg c)=0.∴x+y+z=0,或lg a+lg b+lg c=0.
由lg a+lg b+lg c=0,得lg abc=0,
abc=1,a=![]() ,
,
将①代入axbycz=1,得by-xcz-x=1,
又a、b、c不全为1,只有当y-x=z-x=0.
即x=y=z时,等式成立.
∴填x+y+z=0或x=y=z.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
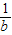 ,b+
,b+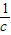 ,c+
,c+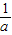 三数中至少有一个不小于2”,提出的假设是( )
三数中至少有一个不小于2”,提出的假设是( )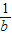 ,b+
,b+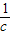 ,c+
,c+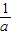 至少有一个小于2
至少有一个小于2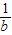 ,b
,b ,c+
,c+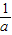 都小于2
都小于2 。
。