题目内容

已知直二面角α-l-β,A∈α,B∈β,如果AB与平面β成45°角,AB在平面β内的射影与l成45°角,求AB与平面α所成的角.

 

解:如图,

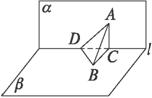
过A作AC⊥l于C,连结BC,则∠ABC=45°.

过B作BD⊥l于D,连结AD,

则∠BAD即为AB与平面α所成的角,且∠BCD=45°.

在Rt△ABC中，BC=AB·cos45°=AB.

在Rt△BDC中,BD=BC·sin∠BCD=·AB·sin45°=AB.

在Rt△ABD中,sin∠BAD==,

∴∠BAD=30°,

即AB与平面α所成的角为30°.


练习册系列答案
相关题目
已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，B∈β，BD⊥l，D为垂足，若AB=2，AC=BD=1，则D到平面ABC的距离等于（　　）
A、
2
3
B、
3
3
C、
6
3
D、1
已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，若AB=2，AC=BD=1，则CD=（　　）
A、2
B、
3
C、
2
D、1
已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，B∈β，BD⊥l，D为垂足．若AB=2，AC=BD=1，则D到平面ABC的距离等于
6
3
6
3
．
（2012•南宁模拟）已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，AC=BD=1，CD=2，异面直线AB与CD所成的角等于
arccos
6
3
arccos
6
3
（用反余弦表示）
已知直二面角α-l-β，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足．若AB=2，AC=BD=1，则CD=
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网