题目内容
设函数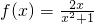 ,
,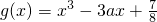 ,若对于任意x1∈
,若对于任意x1∈ ,总存在x2∈
,总存在x2∈ ,使得g(x2)=f(x1)成立.则正整数a的最小值为________.
,使得g(x2)=f(x1)成立.则正整数a的最小值为________.
2
分析:此题考查的是函数的值域的问题.在解答时可以先利用f(x)的条件转化出在 上的值域,然后结合函数g(x)的性质找出函数g(x)在
上的值域,然后结合函数g(x)的性质找出函数g(x)在 对应的范围,从而获的a的关系式,找出a的最小值.
对应的范围,从而获的a的关系式,找出a的最小值.
解答:由题意可知: ,∴
,∴ ,
,
又∵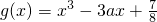 ,且对于任意x1∈
,且对于任意x1∈ ,总存在x2∈
,总存在x2∈ ,使得g(x2)=f(x1)成立.∴
,使得g(x2)=f(x1)成立.∴ 或
或 在
在 上总有解.
上总有解.
所以a的最小值为2.
故答案为:2.
点评:此题考查的是函数的值域的问题.在解答的过程当中充分体现了数形结合的思想、恒成立的思想以及问题转化的思想.值得同学们体会反思.
分析:此题考查的是函数的值域的问题.在解答时可以先利用f(x)的条件转化出在
 上的值域,然后结合函数g(x)的性质找出函数g(x)在
上的值域,然后结合函数g(x)的性质找出函数g(x)在 对应的范围,从而获的a的关系式,找出a的最小值.
对应的范围,从而获的a的关系式,找出a的最小值.解答:由题意可知:
 ,∴
,∴ ,
,又∵
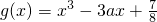 ,且对于任意x1∈
,且对于任意x1∈ ,总存在x2∈
,总存在x2∈ ,使得g(x2)=f(x1)成立.∴
,使得g(x2)=f(x1)成立.∴ 或
或 在
在 上总有解.
上总有解.所以a的最小值为2.
故答案为:2.
点评:此题考查的是函数的值域的问题.在解答的过程当中充分体现了数形结合的思想、恒成立的思想以及问题转化的思想.值得同学们体会反思.

练习册系列答案
相关题目
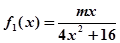 ,
,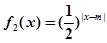 (其中
(其中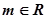 且
且 ).
).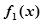 的单调性;
的单调性; ,求函数
,求函数 ,
, 的最值;
的最值; ,当
,当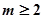 时,若对于任意的
时,若对于任意的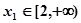 ,总存在唯一
,总存在唯一 ,使得
,使得 成立.试求
成立.试求 的取值范围.
的取值范围.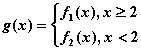 ,当
,当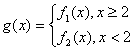 当
当 ,当
,当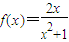 ,
,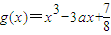 ,若对于任意x1∈
,若对于任意x1∈ ,总存在x2∈
,总存在x2∈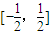 ,使得g(x2)=f(x1)成立.则正整数a的最小值为 .
,使得g(x2)=f(x1)成立.则正整数a的最小值为 .