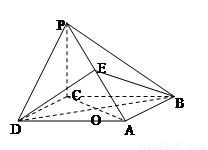题目内容
|
(1)证明:![]() //平面
//平面![]() ;(2)在棱
;(2)在棱![]() 上是否存在点
上是否存在点![]() ,
,
使三棱锥![]() 的体积为
的体积为![]() ?并说明理由.
?并说明理由.
(Ⅰ) 见解析 (Ⅱ) 三等分点
解析:
(1)证明:连接![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,得
,得![]() ∥
∥![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() //平面
//平面![]() . ………………6分
. ………………6分
(2) ![]() 侧棱
侧棱![]() ⊥底面
⊥底面![]() ,
, ![]()
![]() ⊥
⊥![]() ,过
,过![]() 作
作![]() ⊥
⊥![]() =
=![]() ,则
,则![]() ∥
∥![]() .
.
![]() ,
,![]()
![]() , ……12分
, ……12分
![]() 在棱
在棱![]() 上存在点
上存在点![]() 使三棱锥
使三棱锥![]() 的体积为
的体积为![]() ,且
,且![]() 是线段
是线段![]() 的三等分点.
的三等分点.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目


 的底面是平行四边形,
的底面是平行四边形, 平面
平面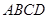 ,
,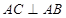 ,
,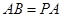 ,
,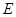 是
是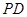 上的点,且
上的点,且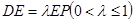 .
.
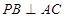 ;
;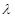 的值,使
的值,使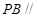 平面
平面 ;
;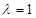 时,求三棱锥
时,求三棱锥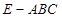 与四棱锥
与四棱锥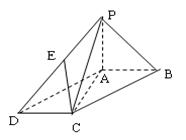
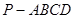 的底面
的底面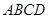 是正方形,侧棱
是正方形,侧棱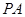
 底面
底面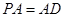 ,
,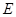 、
、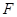 分别是棱
分别是棱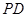 、
、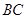 的中点.
的中点. 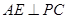 ; (2) 求直线
; (2) 求直线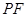 与平面
与平面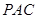 所成的角的正切值
所成的角的正切值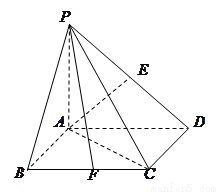
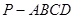 的底面是边长为
的底面是边长为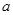 的菱形,
的菱形,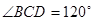 ,
,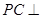 平面
平面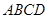 ,
,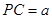 ,
,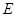 为
为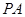 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;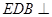 平面
平面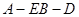 的正切值。
的正切值。