题目内容
设函数 ,其中
,其中 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式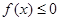 的解集为
的解集为 ,求
,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x-1|≥2.直接求出不等式f(x)≥3x+2的解集即可.(Ⅱ)由f(x)≤0得|x-a|+3x≤0分x≥a和x≤a推出等价不等式组,分别求解,然后求出a的值.
试题解析:解:.(1)当 时,
时, 可化为
可化为 .由此可得
.由此可得  或
或 .
.
故不等式 的解集为
的解集为 . 5分
. 5分
(2)由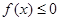 得
得 此不等式化为不等式组
此不等式化为不等式组 或
或 即
即 或
或
因为 ,所以不等式组的解集为
,所以不等式组的解集为 ,由题设可得
,由题设可得 ,
,
故 . 10分.
. 10分.
考点:绝对值不等式的解法.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
三个数 大小的顺序是( )
大小的顺序是( )
A. | B. | C. | D. |
若关于 的不等式
的不等式 在区间
在区间 上有解,则实数
上有解,则实数 的取值范围为 ( )
的取值范围为 ( )
A. | B. | C.(1,+∞) | D. |
设 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为6,则
的最大值为6,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
一只小球放入一长方体容器内,且与共点的三个面相接触.若小球上一点到这三个面的距离分别为4、5、5,则这只小球的半径是 ( )
| A.3或8 | B.8或11 | C.5或8 | D.3或11 |
下列判断错误的是( )
| A.平行于同一条直线的两条直线互相平行 |
| B.平行于同一平面的两个平面互相平行 |
| C.经过两条异面直线中的一条,有且仅有一个平面与另一条直线平行 |
| D.垂直于同一平面的两个平面互相平行 |
 ,
, 是该圆过点P(3,5)的11条弦的长度,若数列
是该圆过点P(3,5)的11条弦的长度,若数列 的解集是 .
的解集是 . 在不等式组
在不等式组 表示的平面区域内部及其边界上运动,则
表示的平面区域内部及其边界上运动,则 的取值范围是 .
的取值范围是 . 