题目内容
20.在△ABC中,A、B、C是三角形的三内角,a、b、c是三内角对应的三边,已知b2,a2,c2成等差数列.(1)求cosA的最小值;
(2)若a=2,当A最大时,△ABC面积的最大值?
分析 (1)由已知利用等差数列的性质可得${a^2}=\frac{{{b^2}+{c^2}}}{2}$,利用余弦定理,基本不等式可求cosA最小值为$\frac{1}{2}$.
(2)由(1)知$A=\frac{π}{3}$,且b2+c2=2a2=8≥2bc,可求bc≤4,进而利用三角形面积公式即可计算得解.
解答 解:(1)∵b2,a2,c2成等差数列,
∴2a2=b2+c2,
∴${a^2}=\frac{{{b^2}+{c^2}}}{2}$,
又∵cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\frac{{b}^{2}+{c}^{2}}{2}}{2bc}$=$\frac{{b}^{2}+{c}^{2}}{4bc}$≥$\frac{2bc}{4bc}$=$\frac{1}{2}$(当且仅当b=c时等号成立),即cosA最小值为$\frac{1}{2}$.
(2)由(1)知$A=\frac{π}{3}$,且b2+c2=2a2=8≥2bc,
∴bc≤4,
∴$S=\frac{1}{2}bcsinA$=$\frac{1}{2}×4×\frac{{\sqrt{3}}}{2}=\sqrt{3}$.
(其他方法合理即可)
点评 本题主要考查了等差数列的性质,余弦定理,基本不等式,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
11.已知a,b,c∈R函数f(x)=ax2+bx+c.若f(1)=f(3)>f(4),则( )
| A. | a>0,4a+b=0 | B. | a<0,4a+b=0 | C. | a>0,2a+b=0 | D. | a<0,2a+b=0 |
8.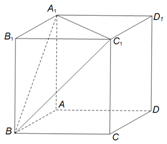 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )| A. | 2π | B. | $\frac{11π}{2}$ | C. | $\frac{16π}{3}$ | D. | $\frac{52π}{9}$ |