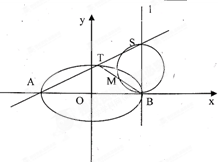
题目内容
设抛物线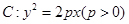 的焦点为
的焦点为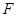 ,准线为
,准线为 ,
,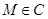 ,以
,以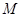 为圆心的圆
为圆心的圆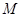 与
与 相切于点
相切于点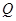 ,
,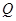 的纵坐标为
的纵坐标为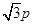 ,
,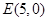 是圆
是圆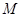 与
与 轴除
轴除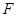 外的另一个交点.
外的另一个交点.
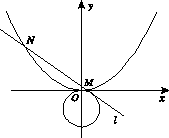
(I)求抛物线 与圆
与圆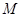 的方程;
的方程;
( II)已知直线 ,
,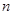 与
与 交于
交于 两点,
两点,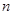 与
与 交于点
交于点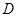 ,且
,且 , 求
, 求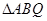 的面积.
的面积.
(I)抛物线为: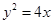 ,圆的方程为:
,圆的方程为: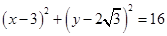 ; ( II)
; ( II) 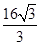 .
.
解析试题分析:(I)根据抛物线的方程与准线,可得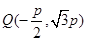 ,由
,由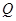 的纵坐标为
的纵坐标为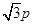 ,
,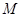 的纵坐标为
的纵坐标为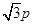 ,即
,即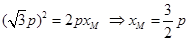 ,
,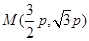 ,由题意可知:
,由题意可知: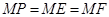 ,则在等腰三角形中有
,则在等腰三角形中有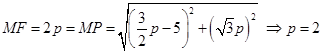 或
或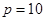 ,由于
,由于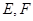 不重合,则
不重合,则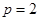 .则抛物线与圆的方程就得出.
.则抛物线与圆的方程就得出.
(II)根据题意可得三角形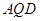 是直角三角形,又因
是直角三角形,又因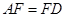 ,则
,则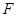 是
是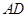 的中点,即
的中点,即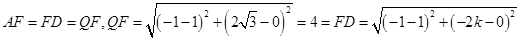 解得
解得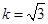 .
.
联立直线与抛物线方程得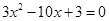 则由弦长公式得
则由弦长公式得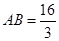 ,又根据点到直线的距离得出
,又根据点到直线的距离得出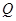 到
到 的距离
的距离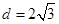 ,从而得出
,从而得出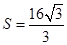 .
.
试题解析:(I)根据抛物线的定义:有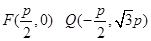 由
由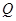 的纵坐标为
的纵坐标为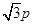 ,
,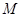 的纵坐标为
的纵坐标为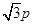
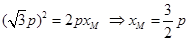 ,
,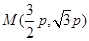 ,则
,则 ,又由
,又由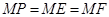 得
得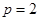
则抛物线为: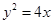 ,圆的方程为:
,圆的方程为: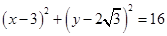
( II)由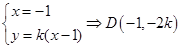 ,
,
根据题意可得三角形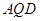 是直角三角形,又因
是直角三角形,又因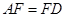 ,则
,则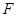 是
是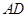 的中点,即
的中点,即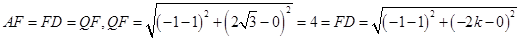 解得
解得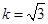 .
.
由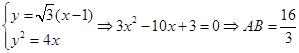 ,根据点到直线的距离得出
,根据点到直线的距离得出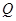 到
到 的距离
的距离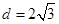 ,从而得出
,从而得出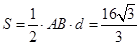 .
.
考点:1.抛物线的定义与抛物线与直线之间的关系;2.对弦长公式与点到直线距离的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
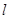 经过点
经过点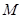 (0,1),且与椭圆交于
(0,1),且与椭圆交于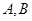 两点,若
两点,若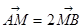 ,求直线
,求直线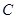 :
: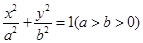 的左、右焦点和短轴的两个端点构成边长为2的正方形.
的左、右焦点和短轴的两个端点构成边长为2的正方形.
 的方程;
的方程; 的直线
的直线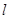 与椭圆
与椭圆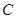 相交于
相交于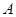 ,
,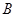 两点.点
两点.点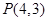 ,记直线
,记直线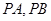 的斜率分别为
的斜率分别为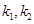 ,当
,当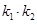 最大时,求直线
最大时,求直线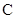 :
: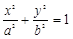 (
(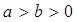 )的右焦点
)的右焦点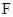 ,右顶点
,右顶点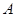 ,右准线
,右准线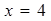 且
且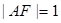 .
.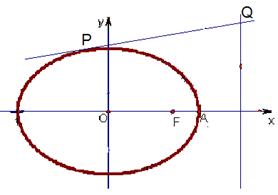
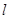 :
: 与椭圆
与椭圆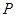 ,且与右准线相交于点
,且与右准线相交于点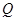 ,试探究在平面直角坐标系内是否存在点
,试探究在平面直角坐标系内是否存在点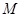 ,使得以
,使得以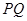 为直径的圆恒过定点
为直径的圆恒过定点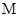 坐标;若不存在,说明理由.
坐标;若不存在,说明理由. 抛物线
抛物线 的焦点均在
的焦点均在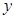 轴上,
轴上,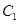 的中心和
的中心和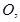 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中:

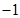
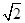
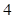
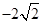
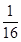
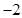
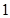
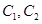 的方程的点的坐标;
的方程的点的坐标;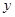 轴上,且过点
轴上,且过点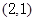 .
.
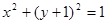 相切的直线
相切的直线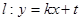 交抛物线于不同的两点
交抛物线于不同的两点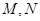 若抛物线上一点
若抛物线上一点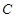 满足
满足
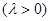 ,求
,求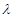 的取值范围.
的取值范围.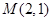 ,平行于
,平行于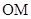 的直线
的直线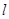 在y轴的截距为
在y轴的截距为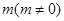 ,且交椭圆与
,且交椭圆与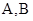 两点,
两点,
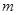 的取值范围;(3)求证:直线
的取值范围;(3)求证:直线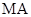 、
、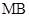 与x轴围成一个等腰三角形,说明理由.
与x轴围成一个等腰三角形,说明理由.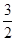 )在椭圆C上.
)在椭圆C上.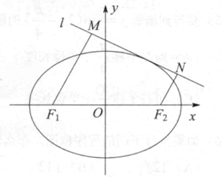
 :
: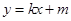 与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且
与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且 ,
,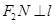 ,四边形
,四边形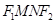 面积S的求最大值.
面积S的求最大值.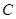 方程为
方程为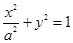 ,过右焦点斜率为1的直线到原点的距离为
,过右焦点斜率为1的直线到原点的距离为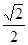 .
.
 为椭圆的左右两个顶点,
为椭圆的左右两个顶点, 为椭圆在第一象限内的一点,
为椭圆在第一象限内的一点, 为过点
为过点 且垂直
且垂直 轴的直线,点
轴的直线,点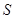 为直线
为直线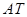 与直线
与直线 为以
为以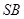 为直径的圆与直线
为直径的圆与直线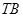 的一个交点,求证:
的一个交点,求证: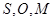 三点共线.
三点共线.